In 2020, Ledger Donjon organised a Capture the Flag contest featuring multiple security challenges covering different types of expertise such as reverse engineering, binary exploitation and side-channel analysis.

A team composed of eShard experts participated in the competition and ranked 3rd at the end of the contest.

In this article, we present a high-level write-up of one side-channel challenge that we solved using Deep Learning.

The challenge

One particular side-channel challenge titled RandomLearn was clearly designed to play with machine learning techniques. The challenge’s synopsis was as follows:

An attacker was able to collect side-channel traces of 200 AES encryptions executed with a secret key that he/she wants to recover. Recovering the key with only 200 traces is hard, however, the attacker was also able to collect a large dataset of 200,000 traces corresponding to the same implementation, but this time with the knowledge of the plaintexts and keys used for the encryptions. The goal is to recover the secret key used for the 200 encryptions executed with the secret key.

As the attack dataset is composed of only 200 traces and that a huge dataset of 200,000 traces with known inputs is provided, the goal is clearly to play with machine learning to reach the solution (even though it is possible to solve the challenge without machine learning). Two machine learning techniques are commonly used for side-channel analysis: Template attacks and Deep Learning-based attacks. In this article we present our solution with Deep Learning.

Disclaimer: We do not claim that the method presented in this article is the best solution to the challenge, and believe that there are most likely simpler and more efficient solutions. In this article, we simply share the methodology and tools that we used to recover the flag in less than 2 hours during the CTF.

Preliminary analysis

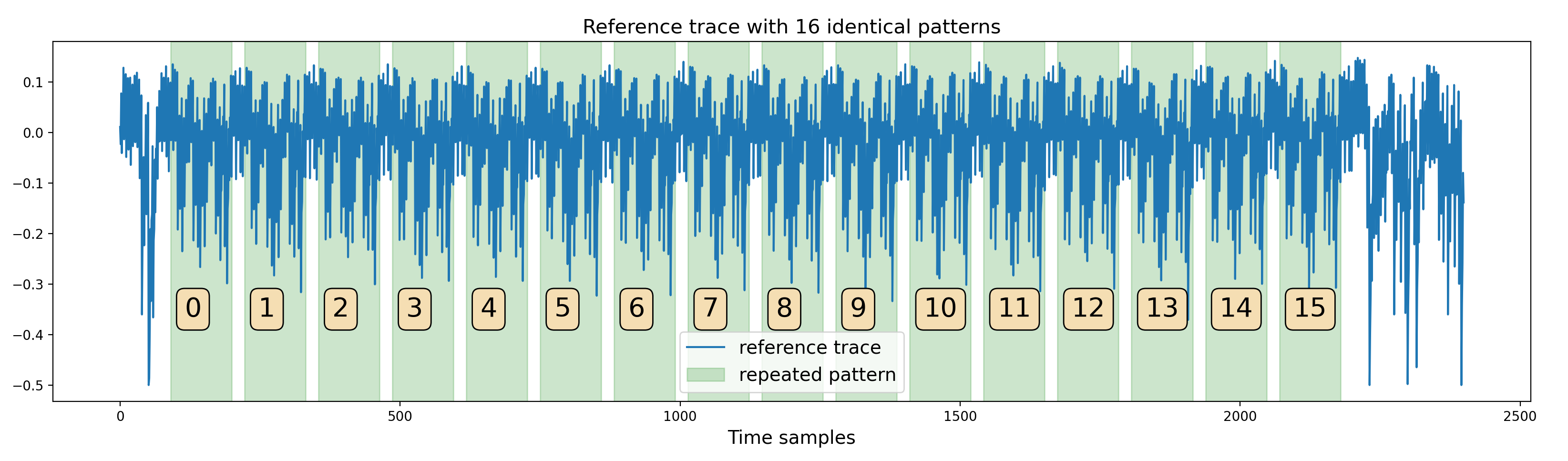
The first step was to better understand the AES signal, detect potential leakages anddefine a strategy to exploit them. A first look at one of the traces shows a series of 16 identical patterns:

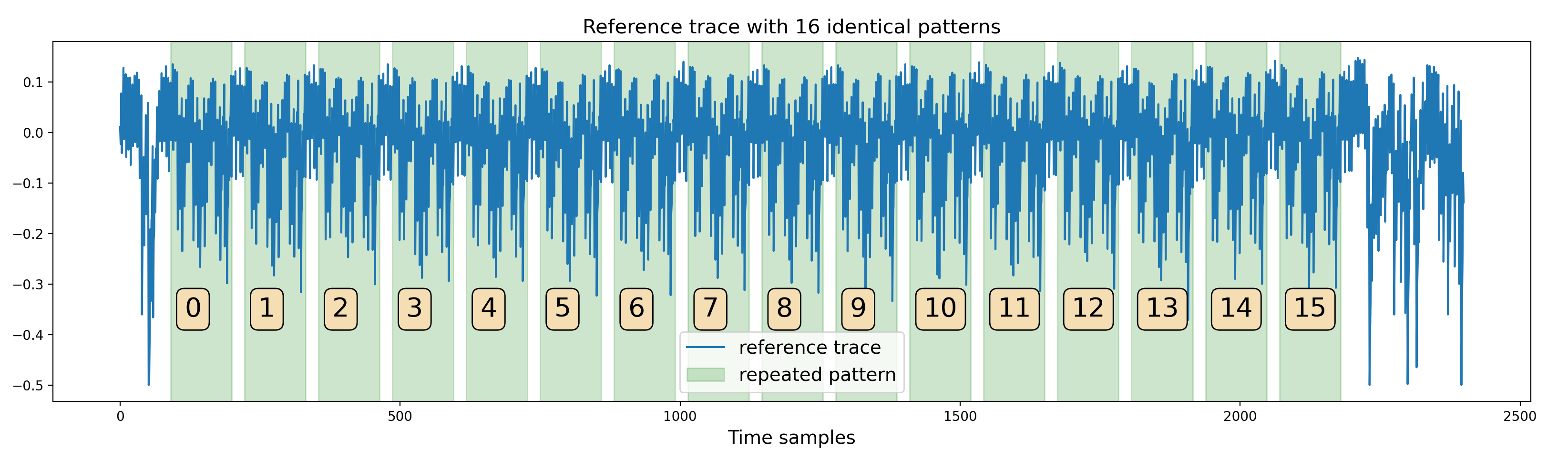
One trace from the dataset

This hints that the trace corresponds to the execution of one operation applied on the 16 bytes of the AES state.

With standard reverse correlation analysis on the learning dataset, it is possible to detect residual leakages of the plaintexts, keys and first round SubBytes output bytes. We therefore rapidly assumed that the collected signal corresponds to the execution of the first round SubBytes operation.

First order attacks do not lead to the recovery of the secret key and leakage levels obtained on the training dataset clearly hint that the implementation is protected, most likely with masking countermeasures.

Deep Learning sensitivity analysis

To further identify and characterize the leakages, we used Deep Learning sensitivity analysis (see for instance the paper [Timon, 2019]) which is a useful technique as it can highlight multivariate leakages.

The idea here is to run a first series of Deep Learning trainings and to compute the sensitivity of the network input during the training to detect the most sensitive input samples. The target

As we assumed that the signal corresponded to the SubByte operation, we decided to first label the traces based on the last byte of the SubBytes output. Besides, we noticed during the experiments that considering the most significant bit (MSB) of the Sbox output byte led to the sharpest sensitivity results.

In esDynamic, we can use the scared open source library to define a selection function and a leakage model that are used to compute the labels from the dataset’s metadatas:

The target

As we assumed that the signal corresponded to the SubByte operation, we decided to first label the traces based on the last byte of the SubBytes output. Besides, we noticed during the experiments that considering the most significant bit (MSB) of the Sbox output byte led to the sharpest sensitivity results.

In esDynamic, we can use the scared open source library to define a selection function and a leakage model that are used to compute the labels from the dataset’s metadatas:

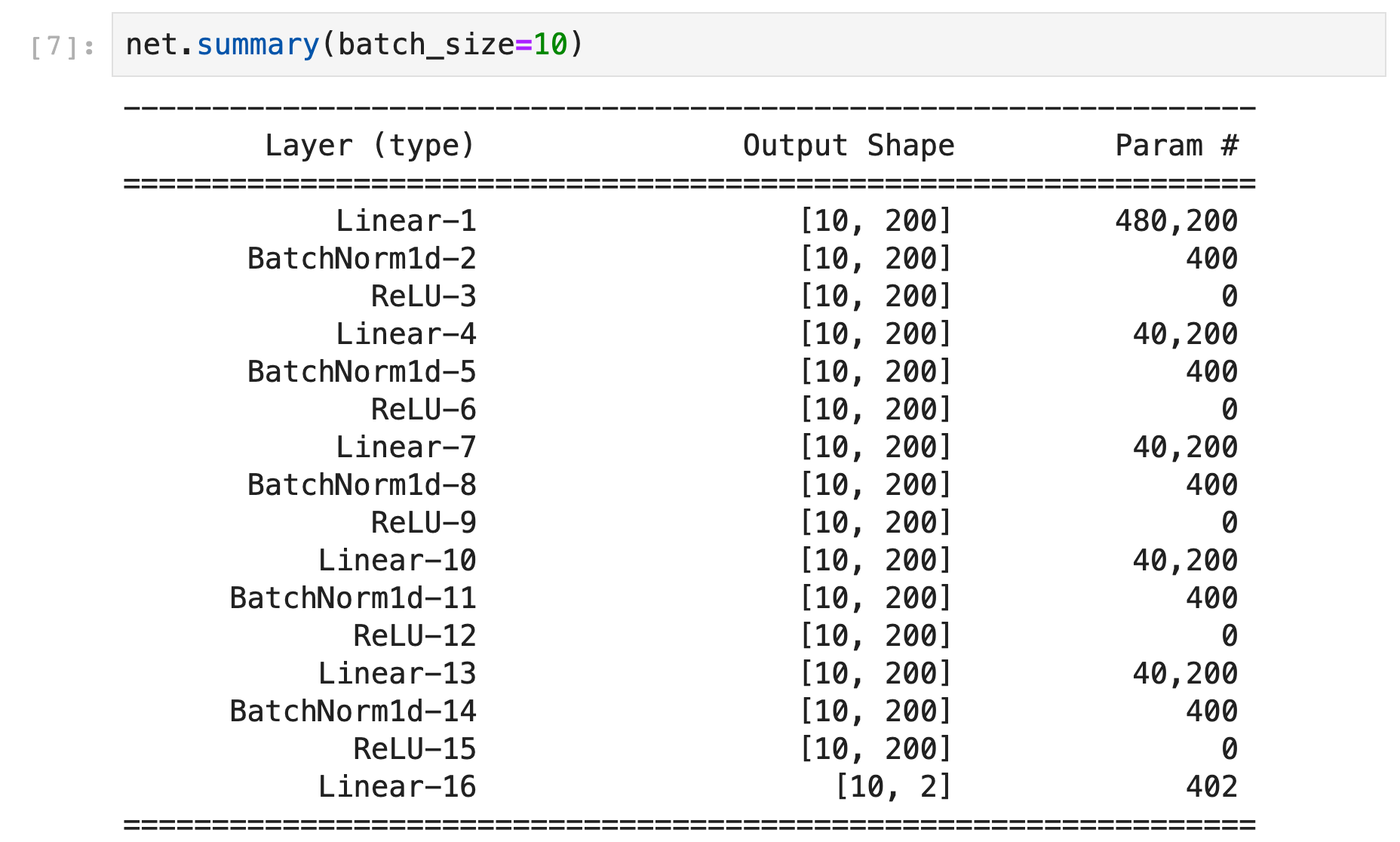
The network We decided to start with a network architecture from the literature, namely the “ASCAD-MLP-Best” architecture, defined in the paper [Prouff et al., 2018].

When starting to work on a new dataset, it makes sense to start running preliminary experiments with architectures from the state of the art and subsequently try other architectures if needed. For this challenge, it ends up that this simple Multi Layer Perceptron (MLP) architecture is sufficient to learn the targeted features and recover the flag.

In esDynamic, one can import this architecture from a collection of several pre-defined networks that can be easily imported and used in the esDynamic notebook environment:

The network is composed of 5 hidden layers of 200 nodes. We slightly adapted the architecture for the challenge:

• As we used a monobit leakage model, the network was here composed of only two output nodes, instead of 256 in the original paper.
• Besides, we added batch normalization layers to the network to stabilize and optimize the training process.

Computing input sensitivity

In esDynamic, it is possible to define Deep Learning SCA experiments in a few lines of code using a dedicated Deep Learning Side-Channel library called esdl developed by eShard.

From a dataset and a neural network instance, one can define a Trainer object to train the neural network with parameters defined by the user. It is also possible to attach customizable callbacks to the trainer object to execute additional operations at different stages of the training. In this case, we attached a callback computing the sensitivity of the network input at the end of each epoch.

When the training is executed over a few epochs, it is possible to observe two very sensitive areas:

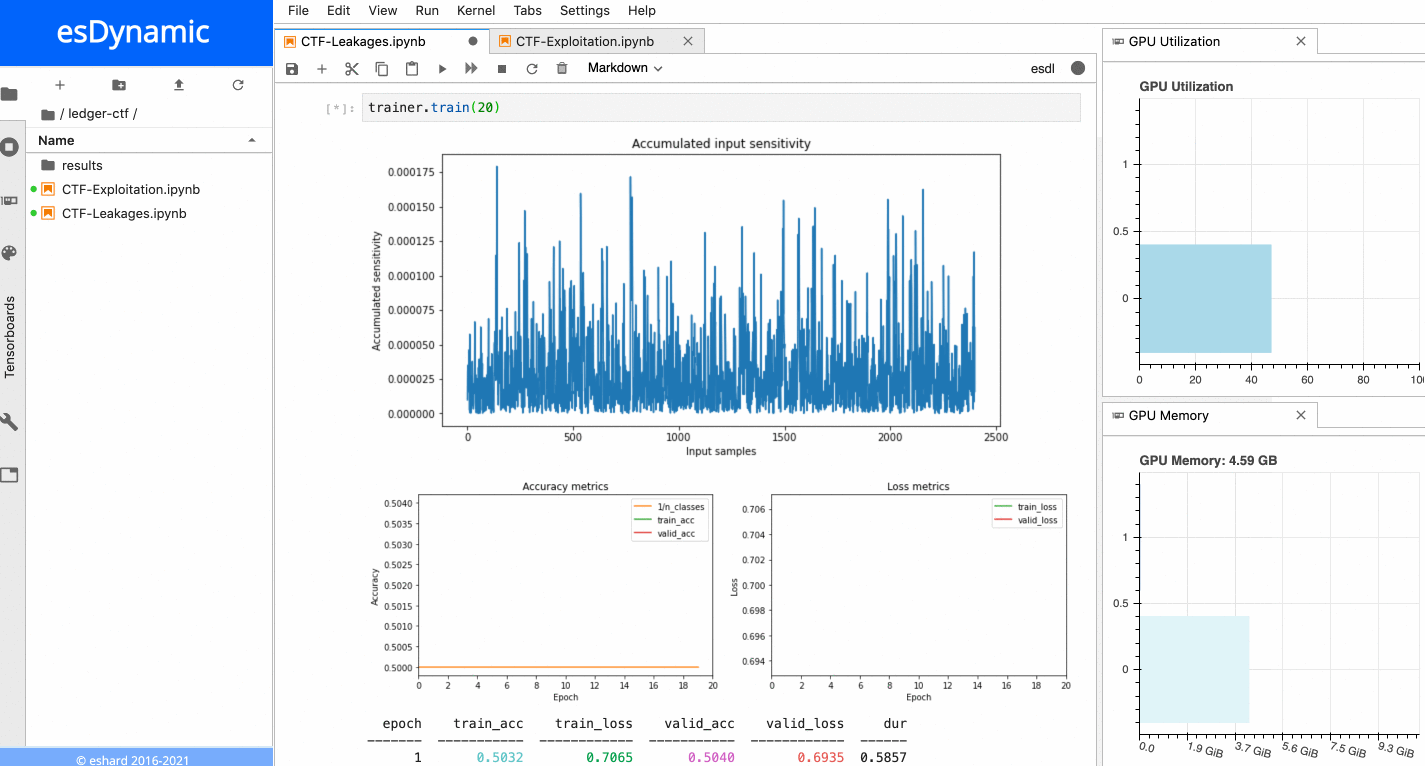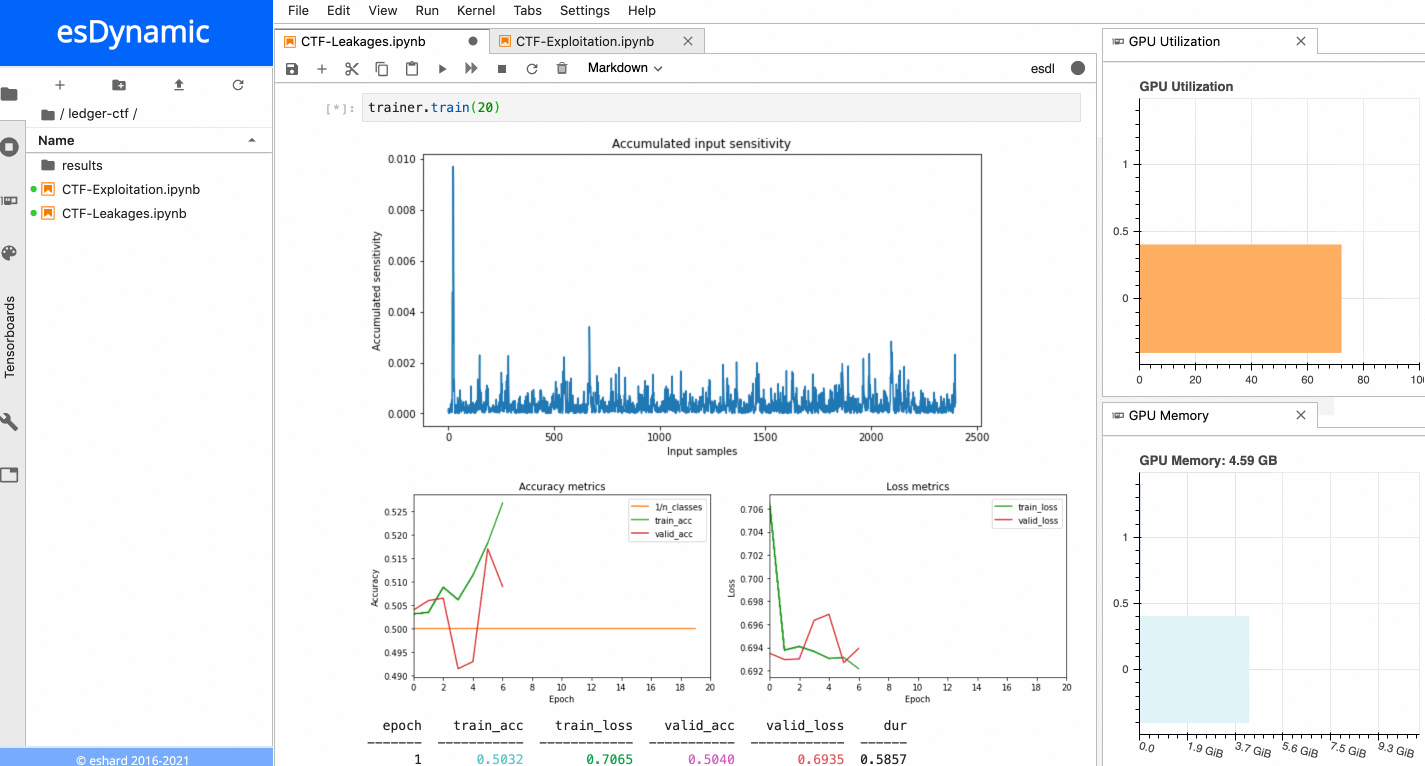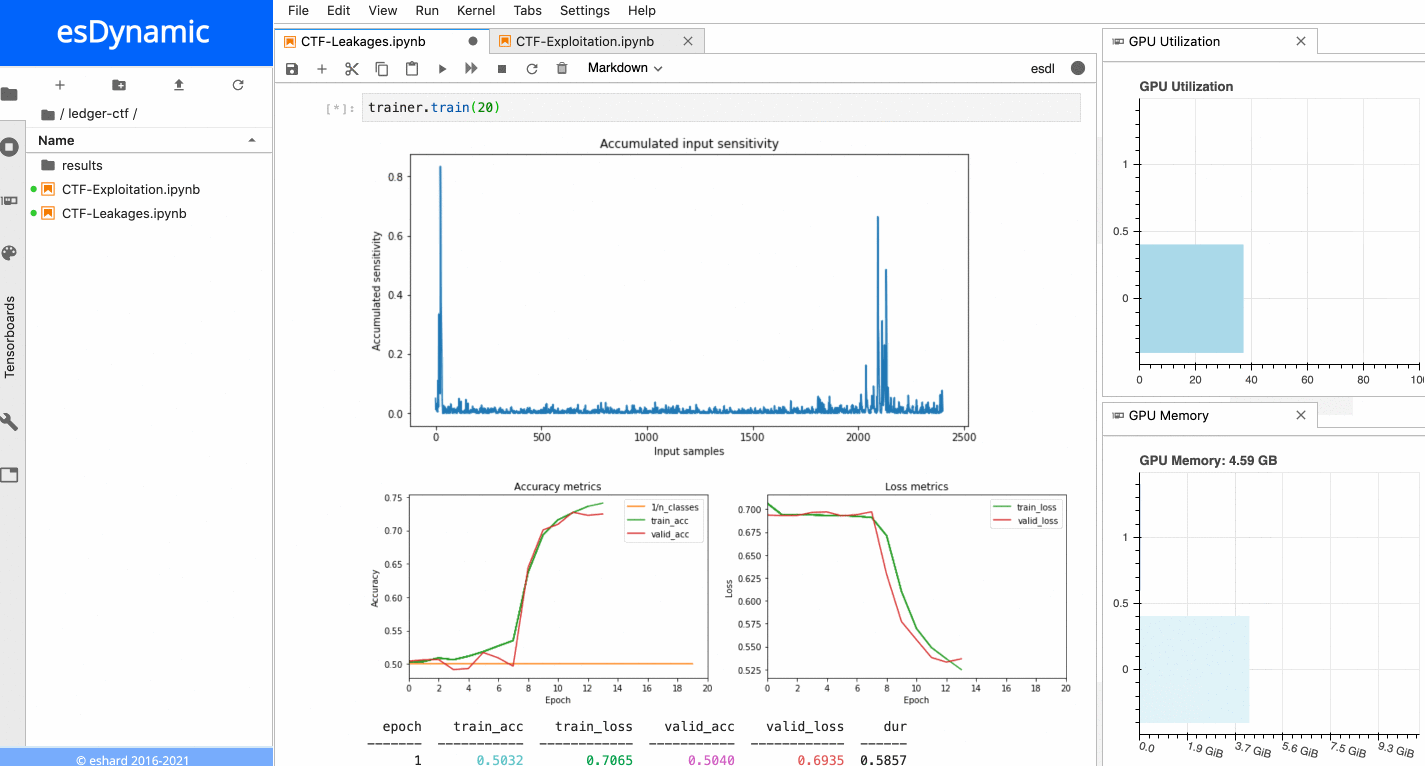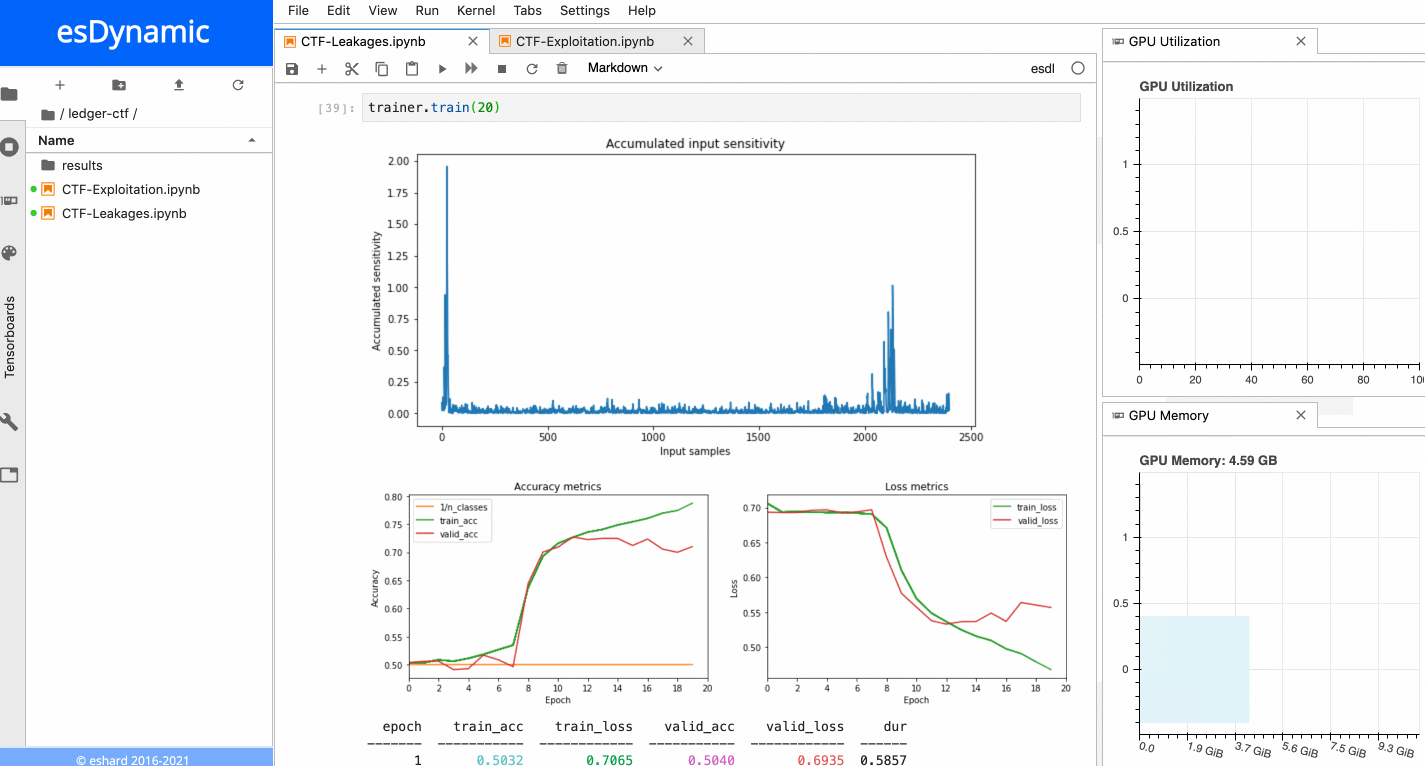
Sensitivity analysis applied on the last byte of the Sbox output.

• The first sensitive area is located at the very beginning of the trace, before the 16 repeating patterns.
• The second sensitive area is located towards the end of the trace, precisely at the position of the last of the 16 patterns, which matches with the index of the targeted Sbox output byte in this example. When a similar process is executed with the other bytes of the Sbox output, it is always possible to observe the first sensitive area at the beginning of the trace, while the location of the second sensitive area depends on the index of the targeted byte. The figure below shows the sensitivity results for both the last byte and the 5th byte of the Sbox output.

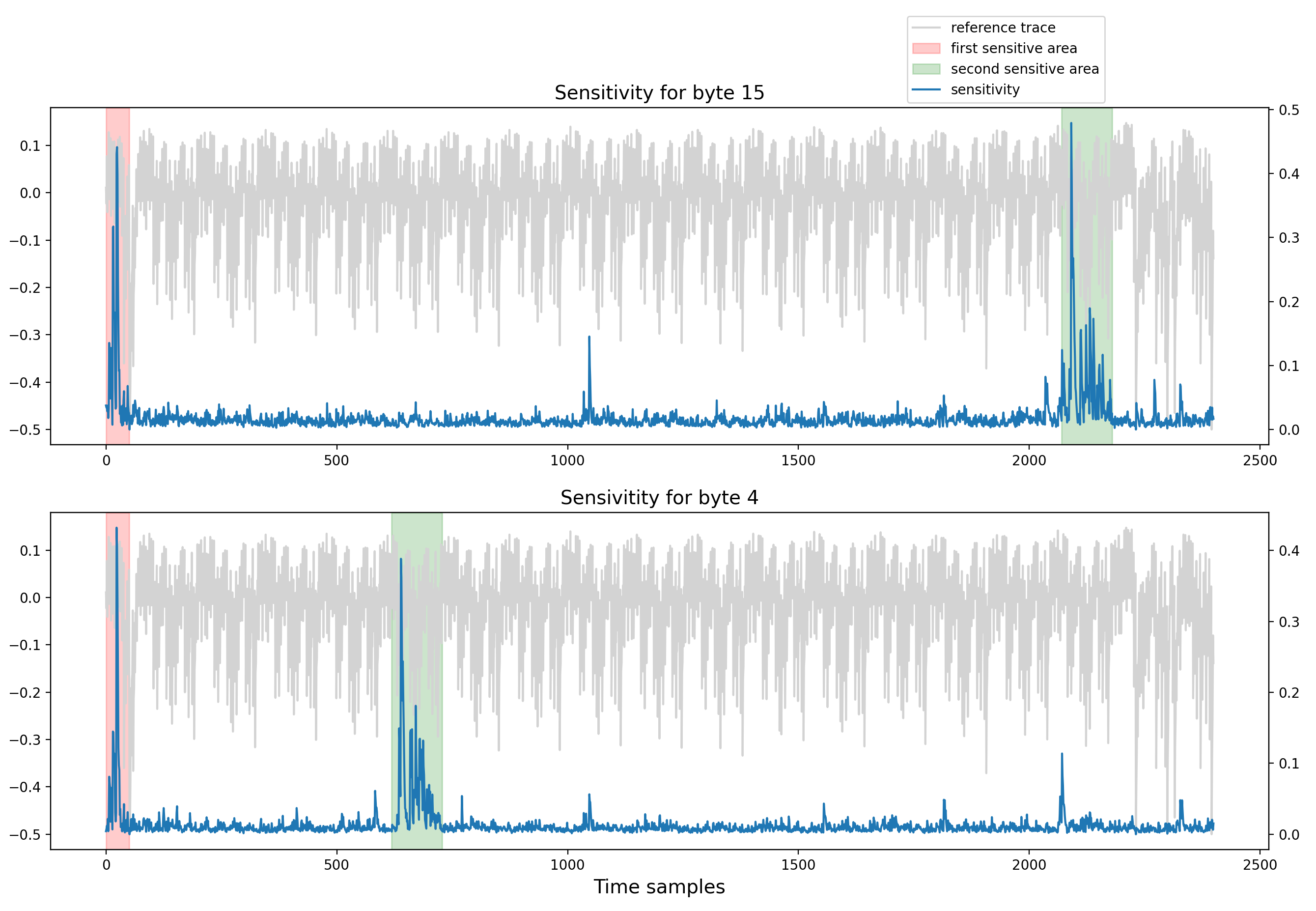Sensitivity results for byte 15 and byte 4 of the Sbox output.

As two sensitive areas are observed, this highlights potential multivariate leakages. One assumption that we made at this stage is that the AES is protected with masking, and that the first leakage area corresponds to the leakage of the mask share, while the second leakage area corresponds to the leakage of the masked Sbox share. This is summarized in the figure below:

Assumption about multivariate leakages areas.

Strategy

At this stage, based on the observations and assumptions presented beforehand, our strategy was to use Deep Learning to exploit the multivariate high order leakages of the SubBytes operation. This strategy was split into steps:

• First, training 16 neural networks using the 200,000 training traces, one network for each Sbox output byte.
• Applying 16 Differential Deep Learning Side-Channel attacks on the 200 attack traces, to recover the 16 bytes of the AES key.

Training 16 neural networks To simplify the training process, we decided to focus the training of each neural network on only the corresponding leaking samples. For each targeted byte, we focused the training on 160 samples, where:

• The first 50 samples correspond to the mask share at the beginning of the trace.
• The other 110 samples correspond to the second leaking share whose location depends on the index of the targeted byte. Moreover, we noticed that during the attack phase the best results were obtained with labels computed from the Sbox output value without applying any leakage model. Therefore, for the training and attack phases we used 256 labels. We used the exact same network architecture as previously, except that at this stage the networks had 256 output nodes instead of 2 previously.

Distributed learning

In esDynamic it is possible to easily distribute the Deep Learning experiments over multiple CPUs or GPUs.

The animation below presents the training of the 16 neural networks in parallel on an esDynamic server with two Intel Xeon E5–2680 v4 CPUs (56 cores in total) and two GeForce GTX 1080 Ti GPUs. The 16 experiments are distributed onto the two available GPUs:

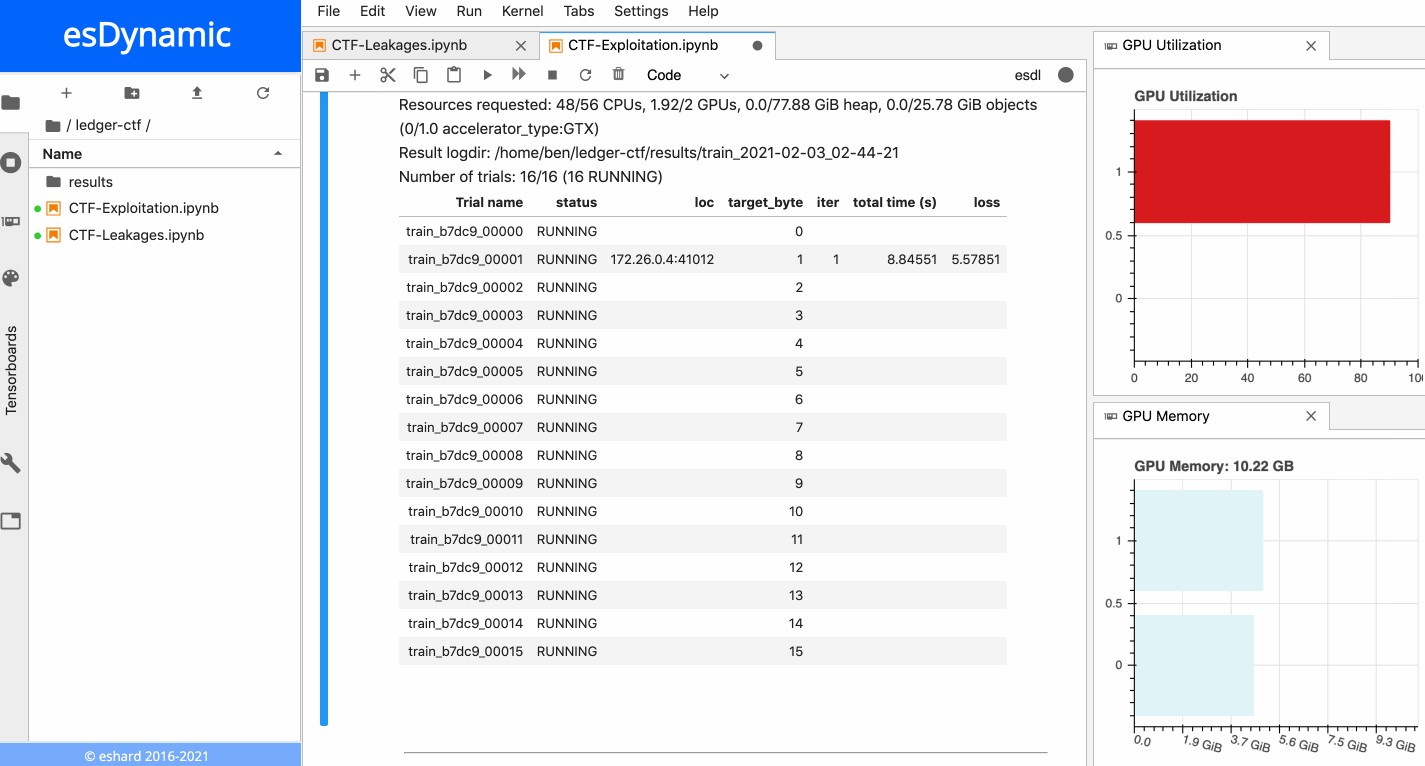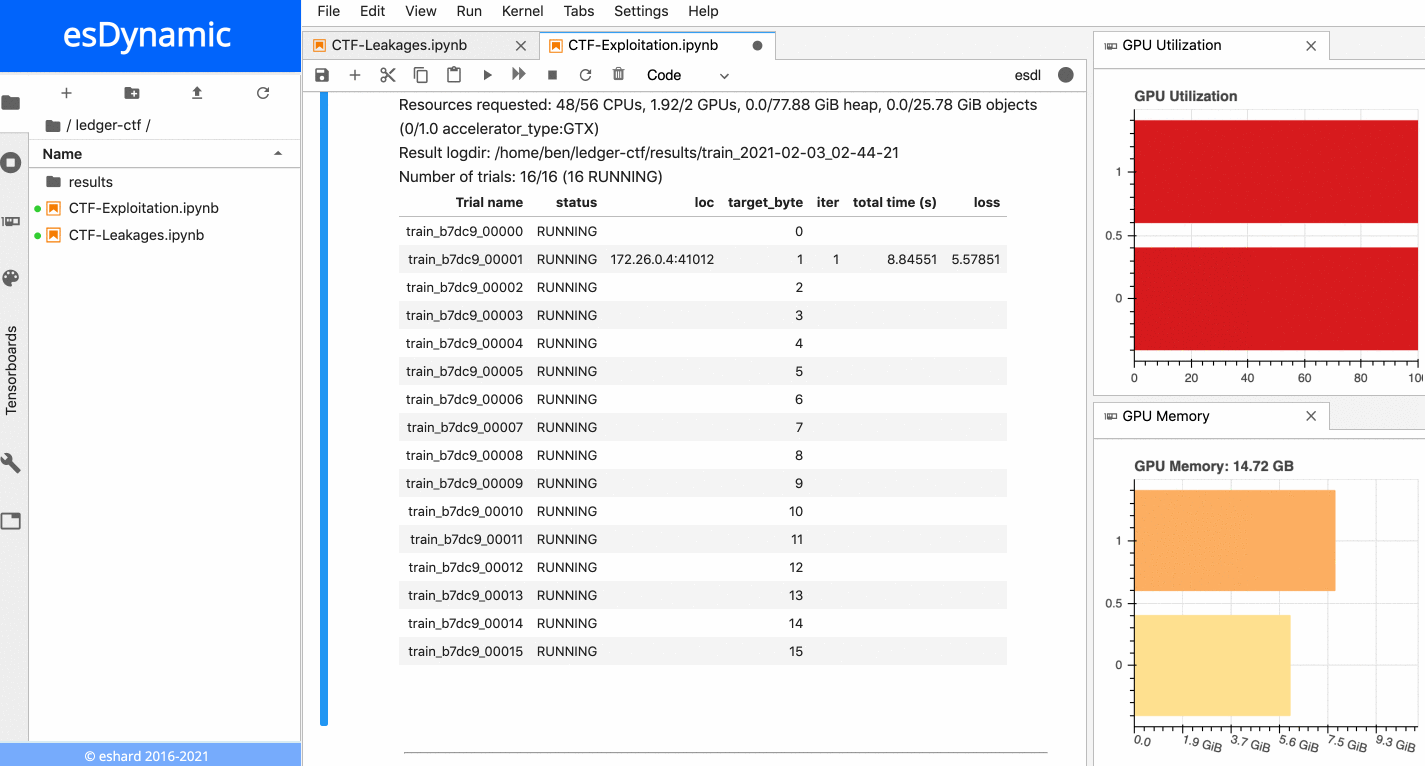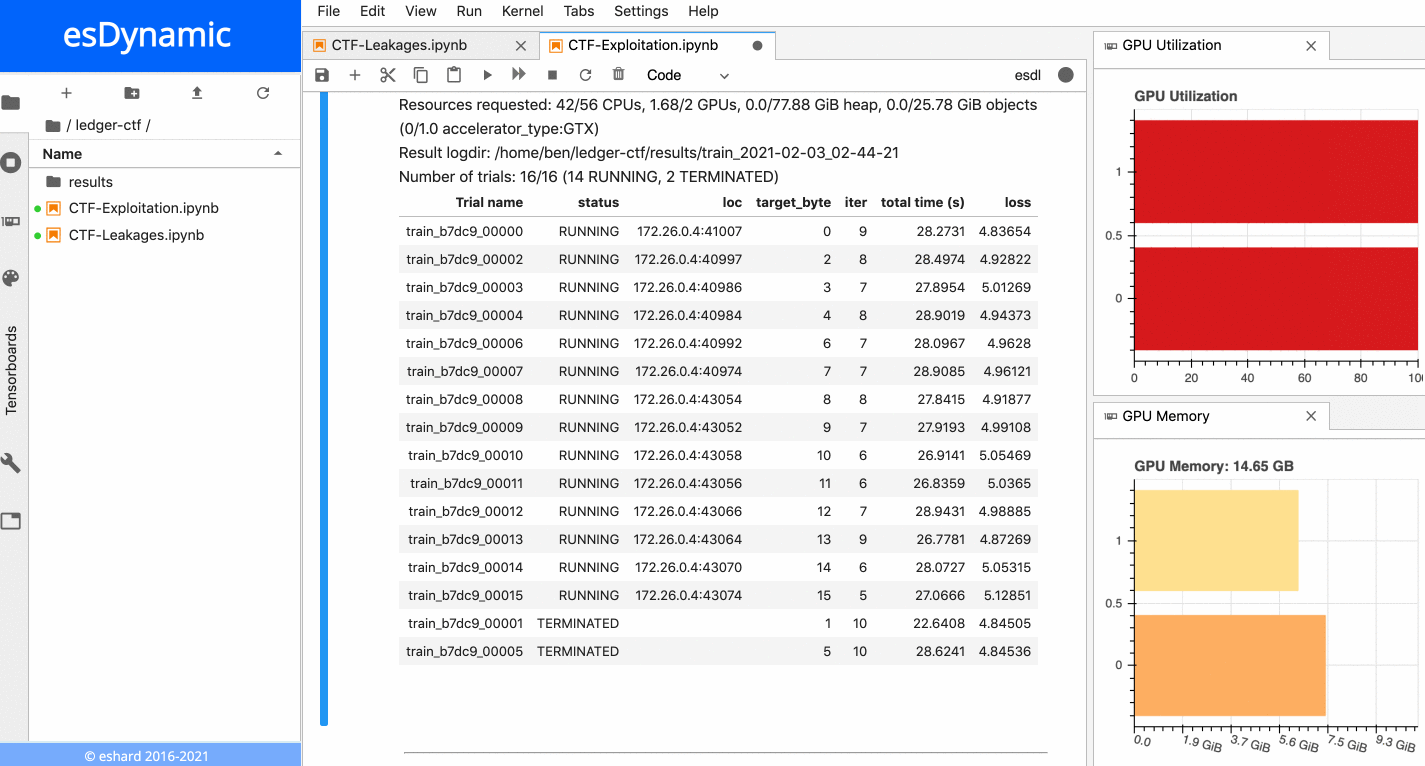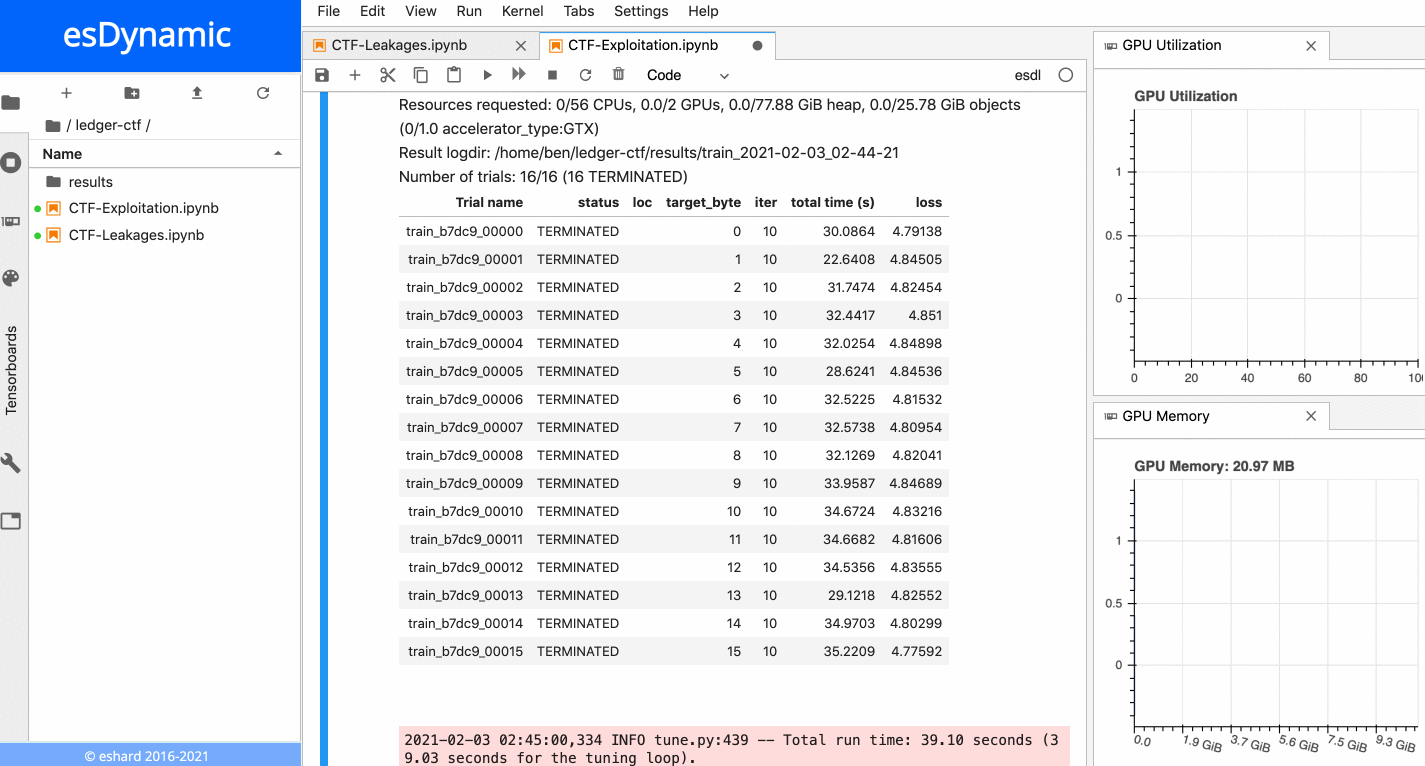
16 neural networks training in parallel on two GPUs.

Each training is executed over 10 epochs with a batch size of 10,000 traces. More details about time execution and performance is provided in a subsequent section below.

Attack

Once the 16 neural networks are trained, we can apply 16 Differential Deep Learning Side-Channel attacks, to recover the 16 bytes of the secret key.

For each of the 16 targeted bytes, the Differential Deep Learning attack clearly highlights one particular key byte leading to higher scores than the other candidates.

Scores of the 16 Differential Deep Learning attacks. The best scores are highlighted in red.

The key recovered by the attack can easily be validated by encrypting one of the known plaintext from the attack dataset and check the result against the known ciphertext. The key recovered at the end of the attack is 5468617473206D79204B756E67204675

Entropy

Below, we present an overview of the entropy of the key during the attack. We provide the actual entropy of the key considering an exhaust with the Score-based Key Enumeration Algorithm (SKEA) as well as the lower and higher bounds of the entropy considering naive and ideal exhaust algorithms.

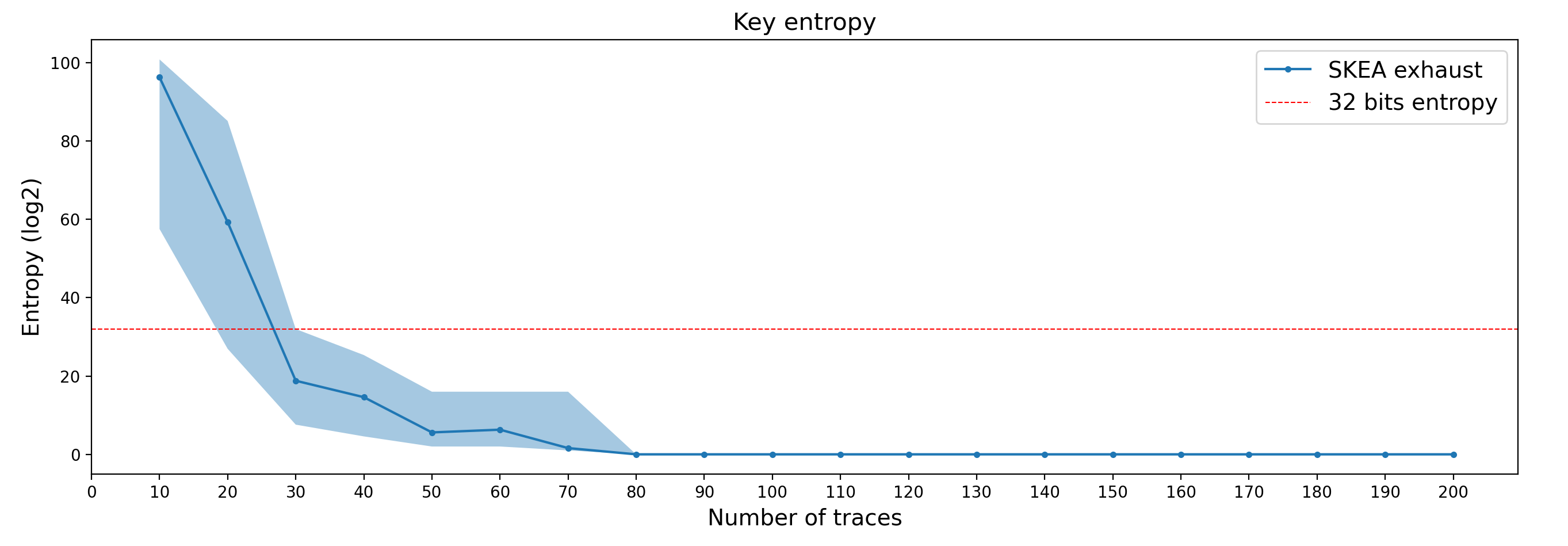
Key entropy over the number of attack traces processed.

We can observe that with 80 attack traces, the key is fully recovered without enumeration. Considering a 32-bit enumeration effort, which represents only a few seconds of enumeration on a standard PC, the key can be recovered with only 30 traces.

Performance

Using a batch size of 10,000 traces, it is possible to process the 200,000 training traces and execute one training epoch in around 0.3 seconds when run on a GeForce GTX 1080 Ti GPU.

Using a batch size of 10,000 traces can be considered quite aggressive, and smaller batch sizes might lead to more stable trainings, however, this approach works and leads to a quick recovery of the flag as experiments can be run very fast. The objective here was to recover the flag as fast as possible during the CTF.

For each of the 16 targeted bytes, 10 epochs are sufficient to train the corresponding network. It means that training each of the 16 neural networks takes only around 3 seconds when each training is considered separately and without including the time required to load the data from disk to GPU.

When the 16 experiments are executed in parallel on an esDynamic server and distributed onto two GeForce GTX 1080 Ti GPUs, it takes** less than 40 seconds** to complete the 16 trainings, including the data loading from disk to GPU.

On the other hand, the attack phase is very fast, as only 200 traces must be processed for inference.

All in all, the whole attack including data loading from disk to GPUs, training the 16 neural networks over 10 epochs and recovering the key, takes less than 45 seconds, when executed on an esDynamic server with two Intel Xeon E5–2680 v4 CPUs and two GeForce GTX 1080 Ti GPUs.

These figures are provided for indicative purposes only and are based on the solution we implemented during the CTF. Again, we are convinced that the challenge can most likely be solved faster with other methods or parameters.

Conclusion

In this article we presented the tool and methodology that we used to solve the RandomLearn challenge of the Ledger Donjon 2020 CTF. We presented how to identify and exploit multivariate leakages in the AES implementation using Deep Learning to recover the secret key with only a few dozen attack traces.

A more detailed write-up of this challenge is available as a set of executable notebooks as part of the Deep Learning module of esDynamic. This module is composed of more than 30 notebooks on Deep Learning-SCA and comes with the dedicated Deep Learning library esdl.

esDynamic provides an open data science environment with the right functionalities to quickly implementDeep Learning-SCA experiments, distribute operations over scalable resources and easily visualize outputs. It is therefore possible for the user to focus on the expertise part of the analysis, rather than on the implementation itself. Using esDynamic and esdl, we were able to solve this challenge in under 2 hours during the CTF, including data preparation, exploration, and execution.

As part of esCoaching, eShard also provides a set of three interactive courses on Deep Learning-SCA, designed to quickly get up to speed on this topic through many practical activities performed on an online esDynamic server with the supervision of eShard experts.

If you are interested in learning more about eShard services and tools, contact us at [email protected] Acknowledgment: We would like to thank the Ledger Donjon team for organizing this nice CTF and for open sourcing its content, therefore providing useful content for the community.

References

• [Timon, 2019] Timon, B. (2019). Non-Profiled Deep Learning-based Side-Channel attacks with Sensitivity Analysis. In IACR Transactions on Cryptographic Hardware and Embedded Systems, 2019(2), pp. 107–131.

• [Prouff et al., 2018] Prouff, E., Strullu, R., Benadjila, R., Cagli, E., and Dumas, C. (2018). Study of Deep Learning Techniques for Side-Channel Analysis and Introduction to ASCAD Database. code block