'Scared': Better, Faster, Stronger

About a year ago, I wrote on the importance of performances for Side-channel attacks here. I claimed, among other things, that our open source side-channel library scared has good performances. Indeed, after some tests it appeared that the computing performances of scared are good compared to other tools. A bit later I open sourced the benchmarking suite I used for testing... But I missed one tool!

Few days after the blogpost and the announcement at the CHES rump session, we received an email from the SCALib developers saying (I summarize): "Why is your library so slow to compute SNR, do I miss something?". And he was right:

• I missed the scared vs SCALib comparison
• SCALib is incredibly fast to compute SNR

I cannot lie, it triggered me but also gave me great motivation to make scared faster!

Faster

We already knew that the partitioned distinguishers in scared are not optimal.

Partitions?

A partitioned distinguisher is a class of distinguishers that, as its name suggests, partitions the traces samples according to the target intermediate values and model.

Here is how partitioned attack (here ANOVA) can compare to the more classical correlation based distinguisher:

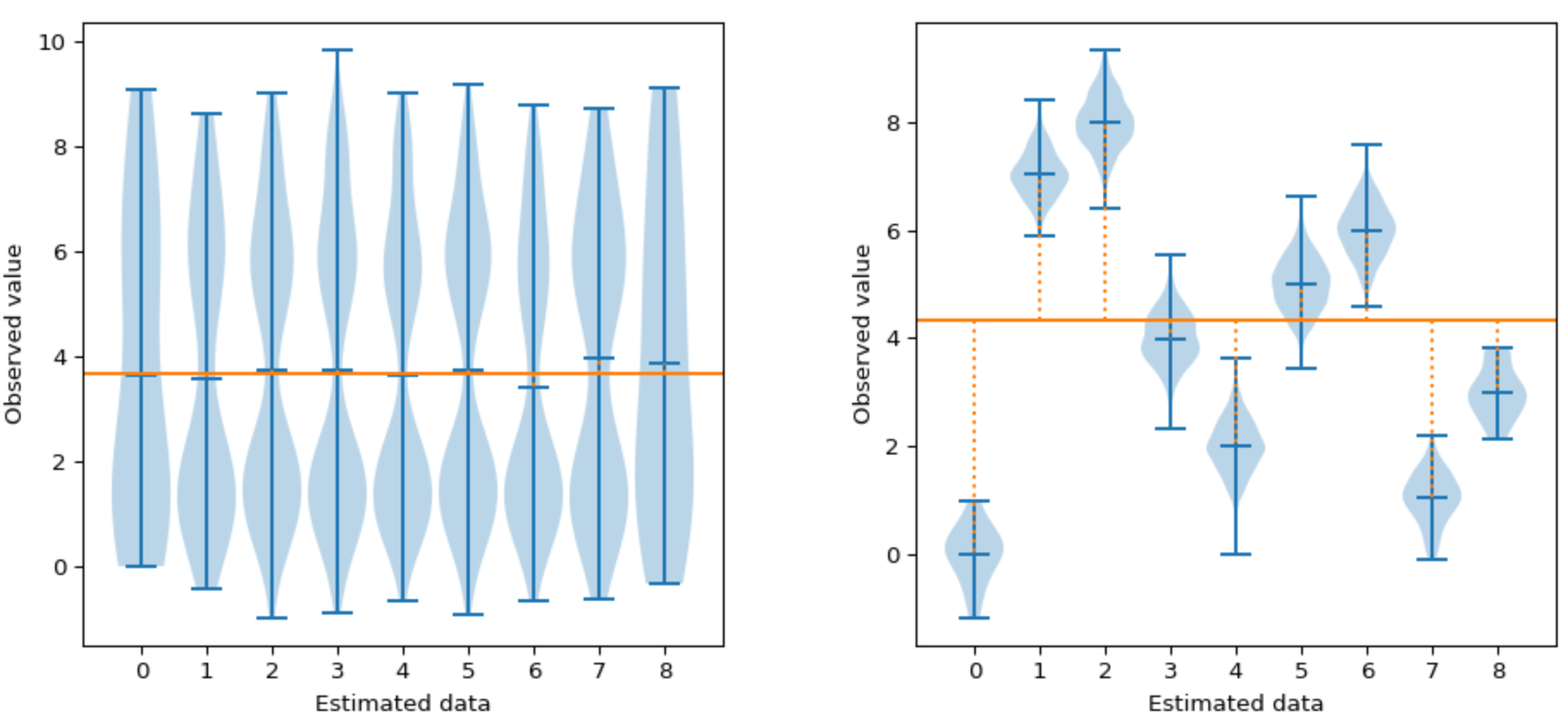
On the left picture shown above, even though our groups are different, neither the CPA or the ANOVA can detect the leakage as there is no variation in the means (similar mean between and within the groups).

On the right-hand side, the CPA still cannot detect leakages as there is still no linear variation of the mean between the groups (inter-group). However, the ANOVA can reveal leakages as there are distinct means between the groups (inter-group).

Scared under the hood...

Let's take another example, the SNR distinguisher targeting the plaintext with the Hamming weight leakage model will compute, for each byte of plaintext as follows:

• the number of traces corresponding to a plaintext word equal to respectively 0, 1, ..., 8
• the sum of traces corresponding to a plaintext word equal to respectively 0, 1, ..., 8
• the sum of squared traces corresponding to a plaintext word equal to respectively 0, 1, ..., 8
• at the end, these values are used to compute means and variances to compute the SNR

The previous scared method to compute partitions was the following: _(below is an example for a single data word, the principle is the same by adding as many columns as attacked byte, 16 bytes for instance):

• compute a Boolean matrix for each trace and each data partition , with if the value of the data word corresponding to trace is equal to partition (see scared code)
• with the samples matrix ( is the sample of trace ), perform the dot product (see scared code)

By doing so, is the sample of sum corresponding to partition .

This method is a lazy way to take advantage of multithreading, as the dot product with numpy, when well configured, is a very efficient operation. However, it's easy to understand that it's not optimal, as a lot of multiplications by zero are performed. And this becomes a real drawback when the number of zeros in the Boolean matrix increases. This is the case when using the Value model, leading to 256 partitions.

SCALib under the hood...

On the contrary, SCALib uses a "straightforward" loop to iterate on each trace, sample, partition and data word. For those familiar with Rust, the code is here. Rust has natively the capability to perform parallel loop while being threadsafe. However SCALib suffers from some drawbacks, especially it can process only int16 data, that can be a problem when traces are preprocessed, leading to float data. Then to do a fair comparison, the conversion time must be taken into account. On a SNR computation, with the Value model (the worst case for scared), SCALib was 45 times faster compared to scared, and this value goes up to 225 time if the conversion time is omitted.

This fact motivated us to make scared faster. For the three available partitioned distinguishers, namely SNR, NICV and ANOVA, the partitioning process was reworked. A new method is now implemented, using parallel loops accelerated with numba. But this new method is not the fastest one in any cases, especially when the number of partitions is low. This is why the loop method coexists with the matrix multiplication one and the fastest method is chosen at runtime. Doing so, we are filling the gap with SCALib, which is now "only" 7 times faster than scared (compared to 45 to 225 times!!). We will probably not rewrite scared using Rust, but we will probably make SCALib compatible with our framework and make it available a new distinguishers for scared.

See below a comparison before / after the code optimizations. This benchmark was performed with the following dataset and setup:

• 25GB dataset, with 1 Million traces of 25,000 uint8 samples, stored on a NVME SSD.
• 16 of the 56 available CPU cores are used (2x Xeon 2680v4)

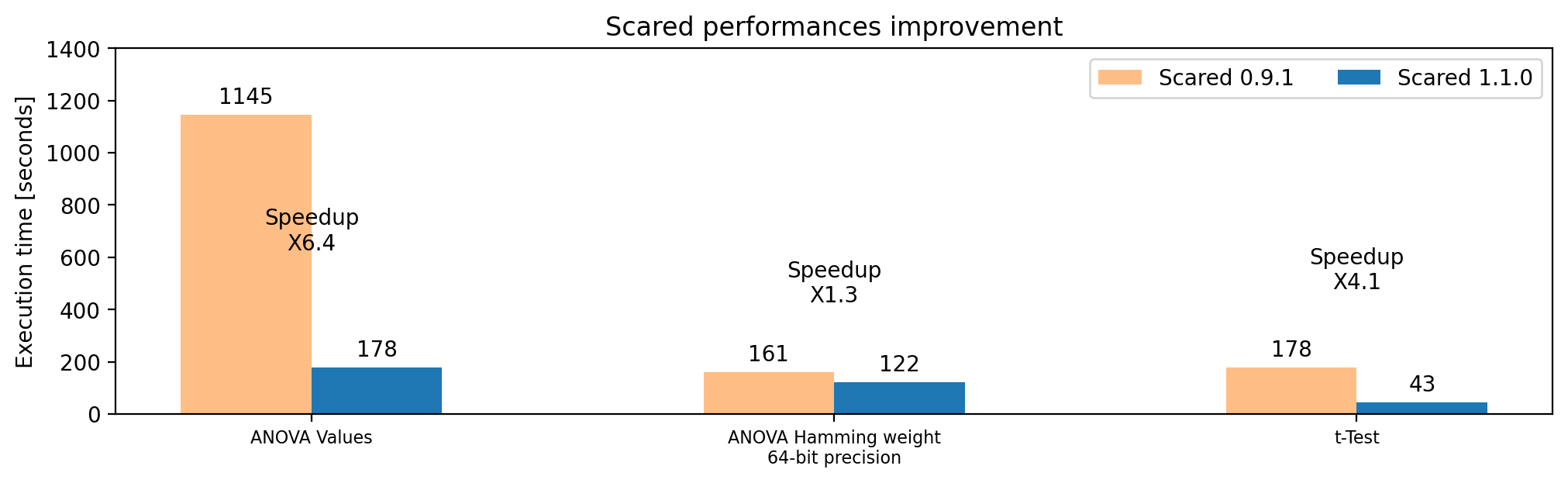Figure - Execution time comparison and speedup, old vs new implementations.

As shown by this figure, the t-Test also benefits from the numba acceleration. To go a step further, another trick was implemented. Indeed, t-Test processes two datasets, and this is now performed in parallel. Combining these improvements leads to a x4 speedup for t-Test computation !

A major speed improvement was also implemented for the MIA distinguisher, with a x50 speedup.

Better

The scared distinguishers allow user to choose the precision used to perform the calculus: scared.CPADistinguisher(precision='float32'). The float64 precision leads to accurate sums, it has the drawback to use twice the memory compared to 32-bit precision. This is why we are mostly using the float32 precision: it saves a lot of memory space and the computations are faster. And the calculus are sufficiently accurate to lead to successful attacks.

Recently we discovered that numpy summation accuracy on float32 arrays depends on the data alignment (see numpy note). After carefully analyzing our framework, we conclude that:

• most of the time, the less accurate sum is used
• the data order processed by the distinguisher depends on the preprocesses of frame used

Obviously this issue was corrected in scared. Now, the data are forced to the Fortran order, which leads to a better precision when the sum is performed on the first dimension (see scared code).

We never encountered issues due to a lack of numerical precision, but in some cases the differences are clearly visible compared to the float64 precision. This is the case on the ASCAD dataset. The following figure shows the correlation according to the Hamming weight of the SubBytes output.

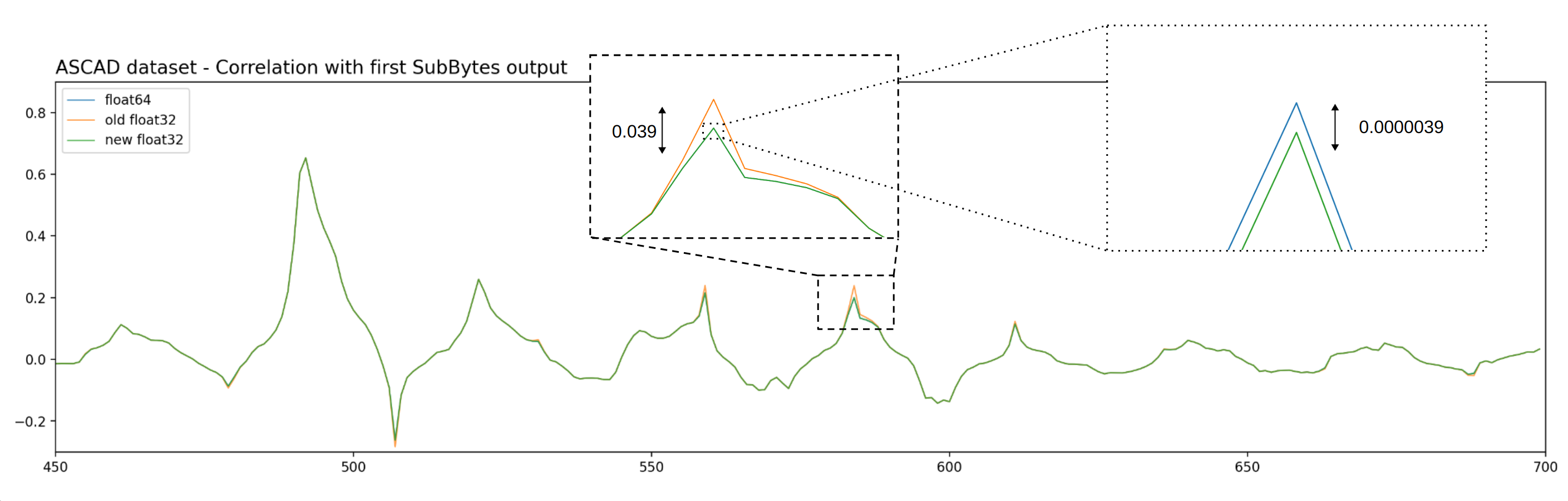Figure - Numerical precision differences.

Using the float64 result (blue line) as a reference, we can see that the error with the "old" implementation (i.e. before the improvements) is clearly visible (orange line) and the deviation goes up to 20% of the reference value. With the new implementation (green line), the error is reduced by a factor 1000.

The counterpart of our new implementation is a small decrease of the computing performances. Indeed, the data are stored on disk in C order and the conversion to the F order is a bit slower compared to converting only the dtype. But it's not a fatality and the open issues on the scared repository show that performance is one of our priorities.

Stronger

As usual when an issue is discovered it is thoroughly studied and fixed. New unitary tests are added accordingly resulting in a more reliable code. In the context of performance, faster execution speed and more efficient resource utilization matters, but in side-channel in particular it shall not be done at the expense of numerical precision.