404CTF “Un point c’est tout” Challenge write-up

Within the eShard intern team, we are eager to learn about security, so we challenged ourselves by subscribing to the 404CTF organized by DGSE and Télécom SudParis. In this article, I will explain how I solved the following one.

My free translation of this challenge:

One point is enough

During a raid on a Hallebarde hideout, your team was able to recover vital information, even though most of it is encrypted. Fortunately, you were able to retrieve a dataset on site, as well as a message exchanged between Hallebarde agents: "Here is the source code of the encryption system we used. I've attached the benchmarks, and I've made modifications you asked me to make. See you tomorrow! Long live Hallebarde!"

The goal is to decrypt the ciphertext that is included in the data.txt file.

cipher_chalenge = 0x76b29ab7d8aad1419e40a46b3e31142a7bcdceaef53ae1fee95f696fea7ff4f2537cb07a397d95334bb7da842640e05abadcc96b225417a011cb36843fb06cb948711fa553243e5eee1e3f5eef0f18f21b553263283309cda6199f29d66cf5f77fc662edc2353da88f562b3be87d287ac998804a729b33430955ca15d5b9595683137334cd245b96fcac4406bfb343e980f9dfaeb28206796b037c88cb7248576d24b73b05c4591d3f32af4caf81dcefbce3422426ac7c5b99f6b6d57675d43162144d12fe31cf9edbfe0f403a23e3766a4eb0a9002265b9ea046bedd26a798d40265ebc7adcfaf1e118eba959bd459eb7a5b79ceb308cf62a3e9f07de7b4d08

TL;DR

After getting the Hallebarde code and the dataset with encryption/decryption timing, I started to analyze these timing in view of a timing attack. I realized that this track is not exploitable. I then explore another attack path based on RSA malleability without success. Finally, back on the timing aspect, I found a special (plaintext; ciphertext) pair that was the point to focus on, and I successfully retrieved the flag with few maths exploiting a well known RSA property.

Challenge material

The main.py file contains all material to generate the key pair, the encryption routine, the decryption routine, and benchmark material to determine the time taken to perform the encryption or decryption operation:

from Crypto.Util.number import getStrongPrime, inverse, getRandomRange
from secret import flag

def encrypt( public_key, pt ):
    N, e = public_key
    return pow(pt, e, N)

def decrypt( public_key, private_key, ct ):
    N, e = public_key
    return pow(ct, private_key, N)

def gen_key( nb_bits ):
    p = getStrongPrime(nb_bits)
    q = getStrongPrime(nb_bits)
    N = p * q
    e = 65537
    d = inverse(e, (p - 1) * (q - 1))
    return ((N, e), d)

def gen_benchmarks( public_key, private_key, f):
    for i in range(200):
        r = getRandomRange(2, N)
        t = time.time()
        ct = encrypt(public_key, r)
        t_int = time.time() - t
        pt = decrypt(public_key, private_key, ct)
        t2 = time.time() - t
        check = (pt == r)
        f.write(
            f'input: {hex(r)}\nencrypted: {hex(ct)}\ntime to encrypt: {t_int}\ntime to decrypt: {t2 - t_int}\nmandatory_check: {check}\n\n')

f = open("data.txt", 'w')

gen_benchmarks(public_key, private_key, f)
encrypted_flag = encrypt(public_key, flag)
N,e = public_key

f.write(f'N: {hex(N)}, e: {hex(e)}\n')
f.write(f'cipher: hex(encrypted_flag)')
f.close()

Part of the data file (full dataset available here):

input: 0x52e20612833e8d5dfc2dfd3ae753e3b7db9773a66fe459174d6cf5d83cc0cf5d7fdb2b0c7a028fc2b232ac5dbde6f097bdf26f61b1180c195af236b39273751281382a1e537b4f3da54fc40d8a1c1f26d510e78665ee617be218f69c76289baaa96ed53aaacaaafd776e6001b638f12bc4e9ff1a08bdd1c7513bd6dfbcf76246c86d9833f85b6aba94cc94bc9cb740752fc5fde004464b86f438d45332ec5efd96e31270d870ee01178b4c02fcdf1b6f329da0e9222aef5e6cfb3363a6be2ee02bb1b5ac957c3c9941f928b0026abe9e0b94f5b349a9efab73a45092b7b1f353b0fae6475ea18934fc31b28293aeae1a1d724cf58731caebbdf07122f81d9afd
encrypted: 0xab229585069162d1aedad58ee9c90dea3a2955abf78e3e8c8925066aaaca096a8fe59138eb7fd7809595bba7564cfdc485b63806b0e9b7e772642a5e26a1f80f630ce85f5c7c10f283dbaf08cdfffbf822e54fcbbe4415e526b428cc7f64a9ce7a0736307bd01d20d9d671d56540e3b14fef3a8dd086431f12696b3195b4b2b30c26b8a19a8991552e5a6864fb7ce7c60514d5fe32d938c352221627ff447613f228b98a59187e46d94d59f6d3ce17136297dcf2d4336807d7fc9e6f1cbfccf6ac9ed91fa66c4cb2dbad9c5153572b86f3901e0908e546b68bb3da9bc9e92da6b92f9e8e74de25cb3e7d4b6ecd3e5521b905ee97d9dede62430748443592b3fb
time to encrypt: 0.0003743171691894531
time to decrypt: 0.030079364776611328
mandatory_check: True

input: 0x7ddba1a407419bfd5ba000a8df196e4be06dd97a8bc53824a3400c69355c00e36e9f62039d803e71016cccfb8f13172d940eefae86d9cf93fb2af14a5904c7be401dfefa66328f98a6bf681fb6bfceb4a2abb3f41476c01b653a77eeb19f574e2535292c7972a2d59ffe3b39c017d0443648ff9e329218b250bf0e0a0175982cd1c0b8dc1a492f8e131fd60822086ef842aff2ee639c868cf014f8e52c19aecd7833bb3c5e54b29130635edd67c6fb97d24edd064b50197ef748770949cf2312e5f4362def04dba459580bed087ed07e059b22b72f07ab0e3b5b4eb705fa75f5203605f3a3714f9415a4b0821a39224850c294e50b6575649d99b6cfa45df4c2
encrypted: 0x285838c4771732e4f12cd939859a335d0808bbe145f1d682c0aac65976bab9ee6b5154caebf2e096ef7e6becfa2896f21bd2a56e0bede2a3a726d744e31aa4da10aeab489f1bbe32c3cd80c18c0a7ad39d13250f76ca34a3345c16b79f49bdffdac219477df5539dbfe351e3d5d706ca71503f1788ea05859fae49f60d519f28aa63238e6fcffa4866c66c62a2f0631e7ba796ffaffac37755b62967beb9a8dc382a9e17db02c1b0c5f1f253eada86b698d47d95599673b1d8a7b481280ad0d1285a9c17ee42f6963062c488e3ac3cf61b478e86e1fbc6420348edc2321f7f606ba0256c15a403305f809de82626fb1e955d52bd998d728b33700cc8a9fcde5b
time to encrypt: 0.00014662742614746094
time to decrypt: 0.021564960479736328
mandatory_check: True

... 197 input/encrypted/timings/checks removed 

input: 0xa573f9775cf9d2de1d5fc3c96aa90328e28583d7e46fb10f61e2fa637efdc215d1607d7c300a33a83f316ceaafb25475a2a88097a347da09f74e849828a585b0a791f9083d2a5c1c287778737662c26e8cf5782e63f3fa8372496210f0a46f1e34f3162a76abf6409053174ee1927081e3d272fa3850c65e6bfb2323ec6226f2bdfc05aa3b3322c7c0ddedcd786db49a8f90e601f96949057bbaa4a317f03abd072fd557256093bb216f35bcfaf0531f129a8770839e5e01d68950003f7248e472fc8e3329d470f4a005c6cf71560b9256f478c1b43261fa8005d78d7225f94e1a3277122ae5540ce721570cfdd08690735cae7bc3c84e5dc89b7df66bd62063
encrypted: 0x98c6758dd9771ca283bb820a813284e7c196108b3c7540d77ecd766676a7a71ea2cfb3de8ebca6d72adcded67ecb8112120d5d953a30f2798a8fb38b1d17ab1e8512d433bb4029ae01e536cd1070f4716616e11f653a1acb4ff1a512255a4406874db4f885434777360f8492b93c21f5ddf85cdb7a0fa9fdd322041c43434e199b8d7c140b035fb200b7a30bf34540bbe2ef3110b570ed23564b05a07da94008322d55487243d36371f62b6610a04b72aab26f7be8a75ed3eb8ebc4d11bd3fdd52b4ecd0c53e1f2a810c9beecbe2c47a695dba902777b61571ffd8335244f90afc6497348f3bb201aa3359d646c7eddbc6e6649ef83013dc581c656212931ee2
time to encrypt: 0.00014591217041015625
time to decrypt: 0.02132582664489746
mandatory_check: True

N: 0xaeba4bba9cabc13627d457decf2fa4ff4b10fcd5cd214821196a3f6de6daa9efb8eb6b70addc690def53a79ca18d2ea889e34379b5f9c9048574521438a27cbe63d0a8033711e1a8e234fba6194dfdea088009ae23fed453e88d424d87cc3354a8a02a3093af02babfaef473279d153bc97d59d88373e29707114c1e413c0552fd9cf9f1a1b3a3f429bdb7158d3fe2e31ac535088f402c6b5c8f59f2b4a2f0c5f95d195322378d2cfaa76a3e66352b95b543677fd8bfc42e474da04e82714d743bc3acd228ae516a9eb8ba51f86d1c256991ad11eef4bb6a953cb8954d62da385feeb8816f88f1e79fdb7b97e4a6035bdf789c42b0fa92a4b5b46449c1df2c9f, e: 0x10001
cipher: 0x76b29ab7d8aad1419e40a46b3e31142a7bcdceaef53ae1fee95f696fea7ff4f2537cb07a397d95334bb7da842640e05abadcc96b225417a011cb36843fb06cb948711fa553243e5eee1e3f5eef0f18f21b553263283309cda6199f29d66cf5f77fc662edc2353da88f562b3be87d287ac998804a729b33430955ca15d5b9595683137334cd245b96fcac4406bfb343e980f9dfaeb28206796b037c88cb7248576d24b73b05c4591d3f32af4caf81dcefbce3422426ac7c5b99f6b6d57675d43162144d12fe31cf9edbfe0f403a23e3766a4eb0a9002265b9ea046bedd26a798d40265ebc7adcfaf1e118eba959bd459eb7a5b79ceb308cf62a3e9f07de7b4d08

Tools and data

First we define functions to parse and retrieve the inputs, encrypted, timing and public key material for data.txt.

def parse_line(line):
    hx = line.split(': 0x')[1]
    hx = hx.strip()
    return int(hx, 16)

def parse_pubkey(line):
    lsplit = line.split(': 0x')
    Nx = lsplit[1]
    Nx = Nx.rstrip(", e")
    ex = lsplit[2]
    ex = ex.strip()
    N = int(Nx, 16)
    e = int(ex, 16)
    return N,e  

def parse_time(line):
    tx = line.split(': ')[1]
    tx = tx.strip()
    return float(tx)

with open('data.txt') as fid:
    lines = fid.readlines()

# Get N, 
pubkey_line = lines[-2]
cipher_challenge_line = lines[-1]
N, e = parse_pubkey(pubkey_line)
cipher_challenge = parse_line(cipher_challenge_line) 

# Remove lines with N, e and c 
lines = lines[:-2]

print("N:", hex(N))
print("e:", hex(e))
print("cipher_challenge:", hex(cipher_challenge))


## Get Plains, Ciphers and related timings

plains = [parse_line(lines[i]) for i in range(0, len(lines), 6)]
ciphers = [parse_line(lines[i]) for i in range(1, len(lines), 6)]
plains_time = [parse_time(lines[i]) for i in range(2, len(lines), 6)]
ciphers_time = [parse_time(lines[i]) for i in range(3, len(lines), 6)]

N: 0xaeba4bba9cabc13627d457decf2fa4ff4b10fcd5cd214821196a3f6de6daa9efb8eb6b70addc690def53a79ca18d2ea889e34379b5f9c9048574521438a27cbe63d0a8033711e1a8e234fba6194dfdea088009ae23fed453e88d424d87cc3354a8a02a3093af02babfaef473279d153bc97d59d88373e29707114c1e413c0552fd9cf9f1a1b3a3f429bdb7158d3fe2e31ac535088f402c6b5c8f59f2b4a2f0c5f95d195322378d2cfaa76a3e66352b95b543677fd8bfc42e474da04e82714d743bc3acd228ae516a9eb8ba51f86d1c256991ad11eef4bb6a953cb8954d62da385feeb8816f88f1e79fdb7b97e4a6035bdf789c42b0fa92a4b5b46449c1df2c9f
e: 0x10001
cipher_challenge: 0x76b29ab7d8aad1419e40a46b3e31142a7bcdceaef53ae1fee95f696fea7ff4f2537cb07a397d95334bb7da842640e05abadcc96b225417a011cb36843fb06cb948711fa553243e5eee1e3f5eef0f18f21b553263283309cda6199f29d66cf5f77fc662edc2353da88f562b3be87d287ac998804a729b33430955ca15d5b9595683137334cd245b96fcac4406bfb343e980f9dfaeb28206796b037c88cb7248576d24b73b05c4591d3f32af4caf81dcefbce3422426ac7c5b99f6b6d57675d43162144d12fe31cf9edbfe0f403a23e3766a4eb0a9002265b9ea046bedd26a798d40265ebc7adcfaf1e118eba959bd459eb7a5b79ceb308cf62a3e9f07de7b4d08

Tracks

Here after the tracks I have followed:

> Investigate the timing track

Well, we are provided with timing... This sounds to send us to the seminal side-channel attack of Kocher on timing. The track is promising, the context seems to fit... But we do not have so many timings to make the attack in practice. Anyway, the computation is operated with the python pow function that uses 5-bit windows on the exponent if the exponent is more than 8 bits long. This means pre-computation… The first computation of the series is longer, certainly because of cache on the working machine. We have to discard it from our analysis. Using the provided code, and from the value of a request with exponent 2 and exponent 3, we can determine the time for a single product on the track of the Kocher classical timing attack. With Kocher's approach, the timing attack will likely determine if a 5-bit window is zero or not, yet it won't be able to recover its value. As a consequence, only if very few non-zero 5-bit windows among the 410 (~2048/5) have to be guessed, we may be able to brute force the exponent. Unfortunately, the variance of the provided timing taking into account the number of 5-bit windows does not indicate a reduced variation of timing compatible with very few non-zero 5-bits windows. The timing information, and our hypothesis of timing attack, our best track, seems to be a dead end.

> Investigate RSA malleability

A well known property of RSA is the malleability, in few words that the cipher of the product of plaintexts is the product of the corresponding ciphertexts. Maybe the ciphertext of the challenge is made of a product of ciphertexts, and so, we can recover the plaintext just by finding the suitable product combination of ciphertext, and then the plaintext will be the product of corresponding plaintexts. But only a few combinations can be tested for complexity reasons.
Following tests were investigated:

• Is the c cipher the product of 2 or 3 ciphers
• Is the c cipher the product of all ciphers
• Is the c cipher the product of all ciphers except one

from tqdm.notebook import tqdm
found = False
l = len(ciphers)
for index1 in tqdm(range(len(ciphers))):
    for index2 in range(index1+1,len(ciphers)):
        res = (ciphers[index1]*ciphers[index2] %N)
        if res == cipher_challenge:
            print(f"{index1} {index2}")
            found = True
if not(found): print("FAIL")

l = len(ciphers)
for index1 in tqdm(range(len(ciphers))):
    for index2 in range(index1+1,len(ciphers)):
        for index3 in range(index2+1, len(ciphers)):
            res = (((ciphers[index1]*ciphers[index2])%N) *ciphers[index3] %N)
            if res == cipher_challenge:
                print(f"{index1} {index2} {index3}")
                found = True
                break
if not(found): print("FAIL")
All = 1
for i, _ in enumerate(ciphers):
    All = All * _ %N
    
if All != cipher_challenge: print("FAIL")

for not_me in tqdm(range(len(ciphers))):
    All = 1
    for i, _ in enumerate(ciphers):
        if i != not_me:
            All = All * _ %N
    if All == cipher_challenge: 
        print(f"Got it {not_me}")
        found = True
if not(found): print("FAIL")

None of them were successful ☹

Back on Timing

In our first steps of analysis, I have used some draws to visualize timing distribution. One of them is a scatter plot using ciphering timing and deciphering timing. I have removed the outlier corresponding to the maximum of cipher timing (that certainly includes the execution cache load), we noticed one point, the red one of short timing for both ciphers and plain computation.

import matplotlib.pyplot as plt
import numpy as np

for x, y in zip(ciphers_time, plains_time):
    x_max = np.max(ciphers_time)
    if x != x_max:
        plt.scatter(x, y)

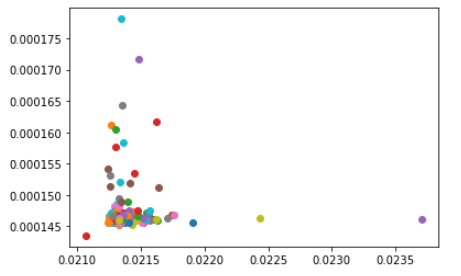
Let’s examine the data related to this shortest timing…

import numpy as np
idxmin = np.argmin(ciphers_time)
print(f"At Index {idxmin}")
print(f"  Plain {plains[idxmin]}")
print(f"  Cipher {ciphers[idxmin]}")

At Index 164
  Plain 20809300321990320180956200183949864693468087251099106043477696862363270172110682334964483785698002096966767229410287316758237759053184208035537331009986896544676710801700948539102086245973407574048015407794108660092938961709197689762521599524845018211701368426681574272178691473036620895633501265437726249423806200276409071823817447551849432441126624765980329355475329009103567904959729574059979410396400369948690126235841790058371527752245622218303683959840684904617024131906463670158401238893946910627168001347466300545234809702998484410841795007741240843630287473438849441161036846380137516556853444920478505091493
  Cipher 20809300321990320180956200183949864693468087251099106043477696862363270172110682334964483785698002096966767229410287316758237759053184208035537331009986896544676710801700948539102086245973407574048015407794108660092938961709197689762521599524845018211701368426681574272178691473036620895633501265437726249423806200276409071823817447551849432441126624765980329355475329009103567904959729574059979410396400369948690126235841790058371527752245622218303683959840684904617024131906463670158401238893946910627168001347466300545234809702998484410841795007741240843630287473438849441161036846380137516556853444920478505091493

A fixed point for RSA is when the cipher equals the plain. For more details about fixed points for RSA you can read here an article explaining more and better this concept.

Fixed points satisfy:

Xe ≡ X mod N ⇔ Xe − X ≡ 0 mod N

or

Xd ≡ X mod N ⇔ Xd − X ≡ 0 mod N

There is two type of fixed points, trivial fixed points which are:

0 , 1 , N − 1 ≡ -1 mod N

And non trivial points which are harder to find:

-1 mod q, -1 mod p, 1 mod q, 1 mod p

Given a non-trivial fixed point F, either F, F+1 or F-1 will be a multiple of one of the secret factors of N.

To obtain the secret factor a simple Greatest Common Divisor (GCD) with N should reveal one of N factors. With one of the factor of N we trivially can retrieve the secret key d.

import math

F = plains[idxmin]

for T in [F+1, F, F-1]: # Two of them are non trivial fixed points
    candidate_q = math.gcd(N,T)
    candidate_p = N // candidate_q 

    if candidate_p * candidate_q == N and (candidate_q != 1) and (candidate_p != 1):
        if T== (F+1) : print("F+1")
        if T== (F) : print("F")
        if T== (F-1) : print("F-1")
        print(f"p: {candidate_p}")
        print(f"q: {candidate_q}")
        p = candidate_p
        q = candidate_q

F
p: 142259697433300919939842401359929747771230586832025361599504948705442285637309595011110242808242610941252894709115956531330752421111628899492037876350866723885700097234304729129112408675903251340080109263483364427005148661660381246459509372077674757697446716575562385199943332804101163273785884074596884905371
q: 155049753042699379284405913334974736081947034453440265765565714632893833266240358819505658549329764196482261772160503174067712120216578902991356315457576279476556108560693053168941159991939763846880402044933872888684753543267474968212439640459297331562744346790242005710055448998081654374865659937687234543437
F-1
p: 155049753042699379284405913334974736081947034453440265765565714632893833266240358819505658549329764196482261772160503174067712120216578902991356315457576279476556108560693053168941159991939763846880402044933872888684753543267474968212439640459297331562744346790242005710055448998081654374865659937687234543437
q: 142259697433300919939842401359929747771230586832025361599504948705442285637309595011110242808242610941252894709115956531330752421111628899492037876350866723885700097234304729129112408675903251340080109263483364427005148661660381246459509372077674757697446716575562385199943332804101163273785884074596884905371

It smells good :-)

# Recover secret exponent from p and q
from Crypto.Util.number import inverse
phiN = (p - 1) * (q - 1)
d = inverse(e, phiN)
# Check with ciphertext and corresponding plaintext
assert pow(ciphers[42], d, N) == plains[42]

🥁 🥁 🥁 🥁

decrypted_flag = pow(cipher_challenge, d, N)
hex_flag =hex(decrypted_flag)[2:]
bytes_object = bytes.fromhex(hex_flag)
ascii_flag = bytes_object.decode("ASCII")

print(ascii_flag)

404CTF{f1x3d_P01n75_4Re_v3ry_C00l}

Thanks

... to DGSE and Télécom SudParis for this CTF! We had a lot of fun working on the different challenges and this one in particular. Indeed, on this one, I spend a lot of time on timing attacks to realize that it cannot help… Malleability was also a wrong track, I realized it later when solving the challenge “Un simple oracle” based on RSA malleability. Happily, Guillaume and Pylou bring me back on the timing analysis with indication to find a special (plaintext; ciphertext) couple within the dataset, so that I found that the shortest timing was such that plaintext = ciphertext and corresponds to a fixed point.