Ledger Donjon CTF Masked Boot write-up

This article presents the solution of the Masked Boot side-channel challenge of the 2021 Ledger Donjon CTF.

The statement of the challenge is the following:

A hardware wallet vendor protects the storage of the user PIN by using firmware encryption. The encrypted user PIN is stored on an off-chip flash memory. After dumping the external flash that contains the encrypted PIN, I managed to control the flash contents and register the power consumption during the power up while the flash decryption was performed. AES-128 algorithm is used inverted in the flash encryption, so the flash encryption "encrypt" operation is AES decrypt and the "decrypt" operation is AES encrypt. Could you help me to extract the PIN?

Introduction

Well, the statement of the challenge is pretty clear. We will attack with side-channel an AES encryption (as here decryption of the flash is performed with AES encrypt). And as suggested by the title masked boot, the encryption is probably protected against first-order side-channel attack and we will need to use high-order techniques.

The challenge comes with the enc_firmware.bin file, which probably contains the encrypted file, and the data.h5 file which contains the recorded power consumption traces.

In the following, we will use estraces and scared, two open source python libraries dedicated to side-channel, to respectively load the data and perform a second order side-channel attack, with the objective to retrieve the AES master key. Finally, the retrieved key will be used to decrypt enc_firmware.bin to get the flag. Note that, as usual in CTF, only the correct key retrieval will lead to a meaningful result, while wrong keys will result in useless garbage.

Open and parse the dataset

The h5 file contains a single dataset aes. Each line of the dataset is composed of two 16 samples long numpy arrays. A first one of uint8 values, which are most probably the ciphered content of the flash. The second one is a float64 array and is probably the recorder power consumption. There is a total of 30,000 lines in the dataset.

The first step is to retrieve the data, from the h5 file, and build the two numpy arrays corresponding to the ciphertext ciphered_data and the power consumption power_consumption. As the size of the dataset if low (4.3MB), this operation is straightforward:

import h5py
import numpy as np

with h5py.File('data/data.h5', mode='r') as file:
    dataset = file['aes']
    ciphered_data = np.array([d[0] for d in dataset])
    power_consumption = np.array([d[1] for d in dataset])
    
print(ciphered_data.shape, ciphered_data.dtype)
print(power_consumption.shape, power_consumption.dtype)

(30000, 16) uint8
(30000, 16) float64

Now we can build a TraceHeaderSet to be used with the scared API. Again, as all the data fit easily in RAM, the process is very simple:

from estraces import read_ths_from_ram

ths = read_ths_from_ram(samples=power_consumption, ciphered_data=ciphered_data)

Second order attack - A Little Bit of Theory

As suggested by the title masked boot, the AES may use a masking countermeasure. Classical masking of AES cipher is the "additive" one, based on XOR operation. The principle is to rewrite AES algorithm to handle only masked data. For each execution, fresh random values (called masks) are drawn and xored with sensitive data before manipulating them. At the end, the masks are removed to obtain the expected ciphered data.

If the masking is well implemented, an attacker cannot predict the values that are really manipulated during the AES computation and then most of the side-channel attack are no more feasible [prouff2013].

A common way to defeat the masking countermeasure is to use a combination function as preprocess of the side-channel attack [Tilllich2008]. This preprocess combines different leakages related to the same mask and, to simplify, acts as a xor to remove the mask. For instance, if the sample is the leakage of the mask and the sample is the leakage of the masked data , combining and reveals the leakage of .

As stated in [Prouff2010], the most efficient combination function for the most classical Hamming weight side-channel leakage is the centered product.

To mount the second order attack, we must find the right selection function, i.e. the AES intermediate data to target. It can be, as explained above, a masked data and its mask or two data masked with the same random mask.

On the safe side, I first tested all the first-order attack paths. None of them resulted in the secret key. So I am pretty sure that masked boot refers to the masking countermeasure. After a few iterations of trial and error, I found that the right selection function is the delta of subbyte output. Indeed, all the bytes of the AES state after the first SubBytes operation are masked with the same mask . For two bytes and masked with , the combination function reveals the leakage of , that can be predicted. However, this attack requires guessing two bytes of key leading to key guesses. But as both the number of traces and the samples per trace are pretty low, so that this attack does not really require a lot of computing power.

Second order attack - Practice

Let me show you how to perform this second order attack with scared.

First, we need to define the custom selection function to target the xor of two bytes after the SubBytes operations. The following function targets only the first two bytes of the AES state.

import scared

@scared.attack_selection_function(words=[0])
def delta_sb_out(ciphered_data, guesses):
    # Compute the SubBytes output for the first two bytes for each of the 256 key guesses
    sbout = scared.aes.SBOX[scared.aes.selection_functions.encrypt._add_round_key(ciphered_data[:, [0, 1]], np.arange(256, dtype='uint8'))]
    # Perform the xor for the 256 guesses of the first byte with each of the 256 guess for the second byte
    result = []
    for i in range(256):
        result.append((sbout[..., 0].T ^ sbout[:, i, 1]).T)
    # Then the results are stacked and a dimension id added to be compatible with the attack API
    result = np.hstack(result)[..., None]
    return result

And we can do the side-channel attack. Classical parameters are used:

• Correlation distinguisher
• Hamming weight model
• Maximum absolute value discriminant to detect the best guess

Obviously, the second order preprocess CenteredProduct is used.

attack = scared.CPAAttack(selection_function=delta_sb_out, model=scared.HammingWeight(), 
                          discriminant=scared.maxabs,convergence_step=3000)

container = scared.Container(ths, preprocesses=scared.preprocesses.high_order.CenteredProduct())
attack.run(container)

We can now display the results. As the number of guesses (and then the number of results) is high, we will display only the first 256 best results. It should be sufficient to see if the attack is successful or not.

import matplotlib.pyplot as plt

best_result_indexes = np.argsort(attack.scores.squeeze())[::-1][:256]
_, axes = plt.subplots(1, 2, figsize=(20, 5))
plt.sca(axes[0])
plt.plot(attack.results[best_result_indexes, 0].T)
plt.title('CPA reusults (256 bests)')
plt.sca(axes[1])
plt.plot(attack.convergence_traces[best_result_indexes, 0].T)
plt.title('Convergence traces (256 bests)')
plt.show()

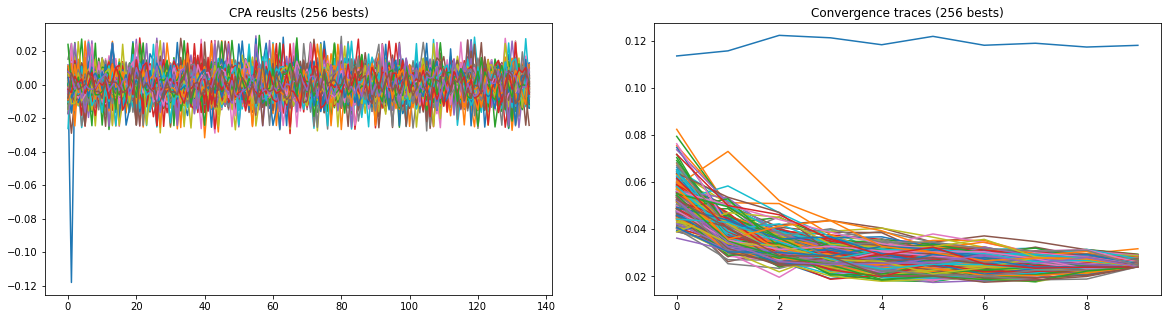
Well, there is obviously a positive result. Let's see to which key guesses it corresponds for each byte:

print("Best key guess for first byte: ", np.argmax(attack.scores.squeeze()) % 256)
print("Best key guess for second byte: ", np.argmax(attack.scores.squeeze()) // 256)

Best key guess for first byte:  101
Best key guess for second byte:  19

Well, the first key byte is retrieved. We will use it to update the selection function and then attack the remaining bytes.

@scared.attack_selection_function(words=list(range(1, 16)))
def delta_sb_out_2(ciphered_data, guesses):
    # Compute the SubBytes output of each byte for each of the 256 key guesses
    sbout = scared.aes.SBOX[scared.aes.selection_functions.encrypt._add_round_key(ciphered_data, np.arange(256, dtype='uint8'))]
    # And then Xor them with the correct value for the first byte
    return (sbout.T ^ sbout[:, 101, 0]).T

attack_2 = scared.CPAAttack(selection_function=delta_sb_out_2, model=scared.HammingWeight(), 
                            discriminant=scared.maxabs,convergence_step=3000)

attack_2.run(container)

We can know extract the best candidate for each key byte and then add the value previously found for the first byte to build the AES master key.

key = np.argmax(attack_2.scores, axis=0)
key = np.hstack(([101], key)).astype('uint8')
key

array([101,  19, 207,  20,  46, 166, 127,  75, 209, 128,  88, 195,  46,
        88, 159, 215], dtype=uint8)

Decrypt the firmware

Then the last step is to use the AES key to decrypt the provided firmware file.

firmware = np.fromfile('data/enc_firmware.bin', dtype='uint8')
decrypted = scared.aes.encrypt(firmware.reshape(-1, 16), key)
decrypted.flatten().tobytes()

b'ics govern where office wheat hint response stay trouble illegal 85269731 \x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x01\x00\x00\x00\x00\x00\x00\x00\x00\x00\x0113371337\x00\x00\x01english\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00'

It works! The final flag is CTF{85269731}.

Thanks

... to the Ledger Donjon team to provide the community with this CTF. It contributes to the emulation of the hardware security community and I'm sure to a better global security. Unfortunately, the eShard team was very busy this year and our collection of collector Ledger wallets is not continuing to grow!

References

[Tilllich2008] Stefan Tillich & Christoph Herbst. (2008). Attacking State-of-the-Art Software Countermeasures - A Case Study for AES. link
[Prouff2010] Emmanuel Prouff & Matthieu Rivain & Régis Bevan. (2010). Statistical Analysis of Second Order Differential Power Analysis. link
[Prouff2013] Emmanuel Prouff & Matthieu Rivain. (2013). Masking against Side-Channel Attacks: A Formal Security Proof. link