The backup superhero of Post-Quantum Cryptography

A new superhero

Let me tell you the story of the newcomer HQC, the latest post-quantum cryptographic algorithm that has been selected by the National Institute of Standards and Technology (NIST) to be standardized. If you've heard of Kyber (or ML-KEM), our first cryptographic Avenger, you'll want to meet its backup superhero: HQC.

Indeed, I have been assigned to study HQC and explain it to the team. Let's be honest, cryptography is not exactly light reading − it's full of abstract math and twisted algebra. But underneath, all that complexity lies a fascinating story: one of mathematical resilience, strategic diversity, and the defense of our digital universe against the rise of quantum computers.

To truly understand how HQC works − not just on paper, but in practice − I decided to get my hands dirty and implement it in Python. Theory is one thing, but building something forces you to wrestle with the details.

So today, we’re sharing that educational implementation hqc-edu with you. It’s not optimized for speed or production use (for that, we recommend checking out PQClean), but it is built for clarity. It walks through the key components of the HQC cryptosystem: from key generation to encapsulation, decapsulation, and even concatenated codes construction, demystifying the inner construction of this post-quantum Key Encapsulation Mechanism (KEM).

The implementation follows the HQC specification as of 2025-08-22 and borrows its notations to ease understanding. I strongly recommend reading the specification alongside this code (you will find more elements on these aspects in the repo’s README).

Part 1: Cryptography heroes

Every universe has its balance, until a cosmic force arrives to shatter it.

In the world of classical cryptography, that balance has long been protected by heroes like RSA, Elliptic-Curve Cryptography (ECC), and AES. For decades, they’ve formed our digital Avengers, shielding everything from messages and emails to bank transactions. They do this by cooperating, RSA or ECC brings our green brute AES, a.k.a. Hulk, to battle and protect these assets. This heroic strategy is called a KEM (Key Encapsulation Mechanism), where RSA/ECC encapsulate a secret key and decapsulate it on the battlefield to unleash the actual encryption with AES.

Part 2: The rise of Thanos

Thanos comes with the power of quantum physics in his gauntlet. Well, the quantum computer isn't just faster than classical computers; it plays by completely different rules. It harnesses the weirdness of quantum physics − superposition and entanglement − to break the foundations of the world of classical cryptography.

Hence, Thanos, armed with Shor's Algorithm, can solve the discrete logarithm problem and the integer factorization problem behind RSA and ECC, respectively, killing Hulk's ride to battle!

Hulk is also damaged! Thus, Thanos can leverage Grover’s algorithm to weaken him and make slightly easier the guess of an AES key − but not by much: We only need to double the key size, i.e., use AES-256. In other words, Hulk gets a scratch, not a K.O..

However, we still have a problem:

In cryptography, AES-256 still needs a secret key to do its smashing − and you have to securely send that key to the other party. Right now, we rely on RSA or ECC to deliver it, but if those are broken by Thanos (quantum computers)... then Hulk never reaches the fight.

Part 3: Keeping our AES Secret Key Secret

In a post-quantum world, we need KEMs that can survive the battle with Thanos. That’s why NIST launched a quest to find post-quantum algorithms − new heroes that can securely deliver AES keys, even under the quantum fire of Thanos!

• Kyber is our first KEM Avenger, Yoda, using the powers of Lattices.
• But today, we’ll talk about its backup hero from another universe − HQC, who brings the powers of error-correcting codes into the fight.

These heroes restore the glory of the KEM strategy that defends the universe against quantum computers: Kyber or HQC + AES-256

Kyber: Yoda of the Lattice Realm

So the first official KEM Avenger is Kyber (now called ML-KEM), the default recommendation from NIST. Kyber is fast, efficient, and built on a mathematical structure called Lattices.

Think of Lattices like alternate dimensions of number space − complex, multi-dimensional grids where mathematical problems become surprisingly difficult for both classical and quantum attackers.

• That’s Kyber’s power: hard Lattice problems.
• Its weapon of choice? The force of the Module Learning-With-Errors (M-LWE) problem is like a spell where small noise hides the secret, and recovering it becomes impossibly hard.

But What If Yoda Fails and Kyber Falls? Enter HQC

As powerful as Kyber is, the cryptographic world has learned not to put all its trust in one hero. We’ve seen attacks evolve. Lattices could someday be broken or weakened − maybe not by a quantum computer, but by clever future attacks.

So NIST wanted backup plans − heroes from other mathematical realms.

That’s where HQC comes into play − Reed Muller-Richards-Solomon from the Fantastic 4, wielding its power not from Lattices, but from the realm of error-correcting codes.

• Don't be afraid, its strength comes from the Syndrome Decoding Problem (SDP) of random Hamming Quasi-Cyclic codes, I will explain later...

Together, Kyber and HQC give us cryptographic diversity − the multiverse of post-quantum defense to deliver that secret AES-256 key and to secure our communications.

HQC

Our superhero story aside, we are going to dive into HQC to bring up its core idea. You can then read the specification and explore our Python implementation to understand exactly how these objects are manipulated.

Let's go slightly inside the mathematical world, so that we will touch the theoretical ground and understand the underlying principle of HQC (Hamming Quasi-Cyclic).

Hamming Quasi-Cyclic codes are a class of error-correcting codes that have an interesting property: message encoding is done through modular polynomial multiplication... sounds daunting, it basically boils down to something we can efficiently compute.

What are error-correcting codes (ECC)?

ECC or not ECC? That is the question

Well, the theory originally aims at solving the following problem: I want to send a message through a physical channel to another party. This channel can be radio-signals, fibre-optic, a rope, ... which in essence will yield errors due to its physical nature. Hence, the received message might be corrupted by some physical effects.

To overcome this issue, we use the ECC mathematical object, shortly code, to encode our message into a larger one called a codeword, which most commonly is a binary version of your message plus redundancy bits. Then, when the codeword is received on the other end of the channel, it is decoded and a certain number of errors, if any occurred, are corrected.

Well-known applications of ECC are:

• Communication with the NASA Mariner spaceship, to retrieve images of Mars, despite the cosmic perturbations

• Encoding of Compact Disc (CD) or Digital Versatile Disc (DVD)

The error-correction capacity of a code is a fundamental metric, usually denoted . This metric is related to the minimum distance between any two codewords: , and conditions the separation of codewords.

So, you can imagine a code and its codewords as points distanced from each other by . Around each codeword, we can draw a circle of radius to illustrate the maximum error-correcting capacity, like this:

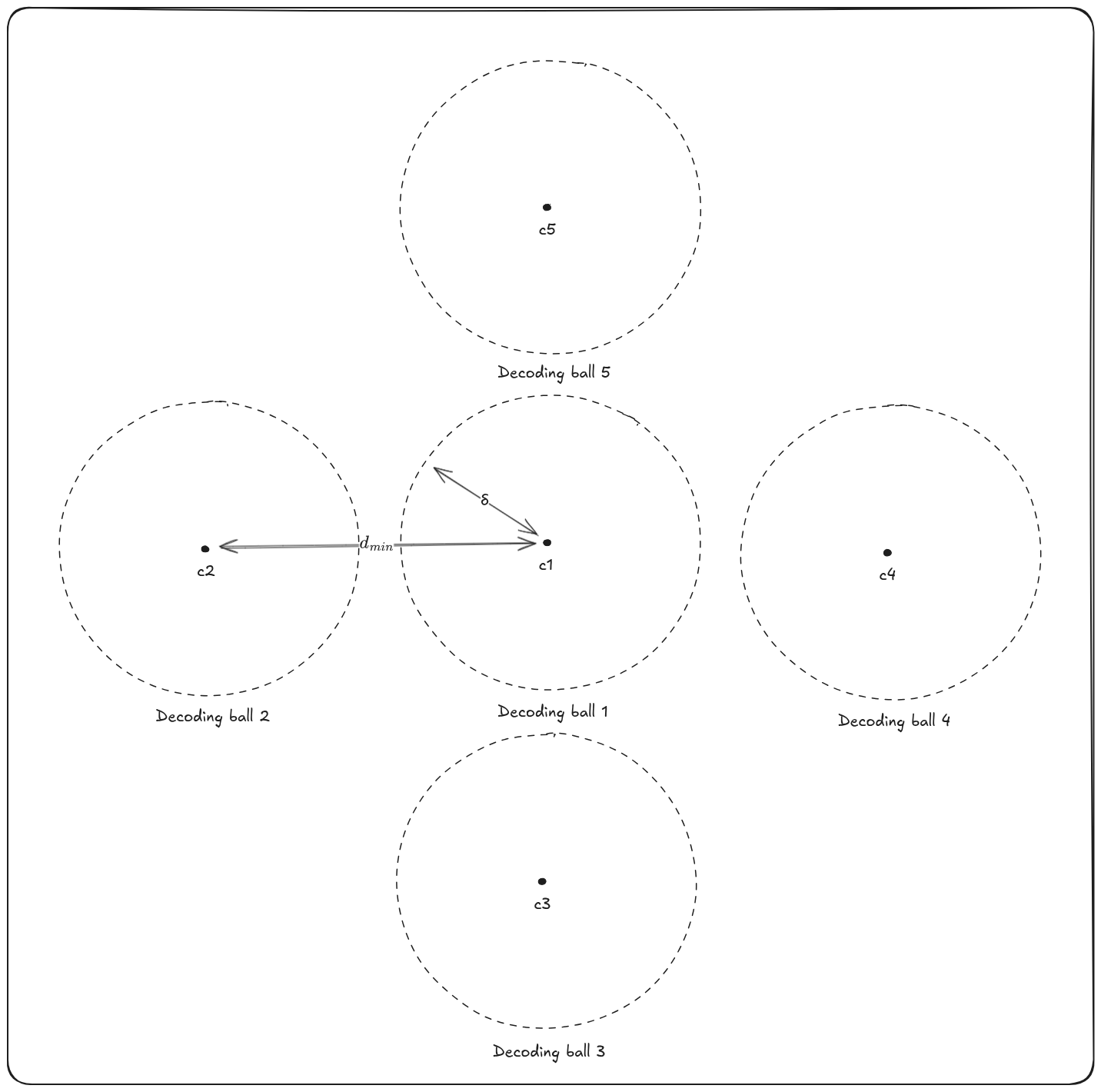
HQC internals

As we stated in our story, HQC is a Key Encapsulation Mechanism (KEM). A KEM is generally built using an encryption scheme: encrypt a message, send it through an unsecure channel, and decrypt it on the other end.

The way HQC does this is very clever. Using a public error-correcting code named , Alice encodes her message and adds an error/mask greater than to the resulting codeword so that it falls out of the initial decoding ball (decoding ball 1 in the animation below). Hence, if someone intercepts the masked codeword, two possibilities arise:

• Either the masked codeword falls in the no man's (decoding) land and leads to a decoding failure
• Or the masked codeword falls into another decoding ball, and decodes a wrong message!

As a result, Alice's message is encrypted = encoded + masked.

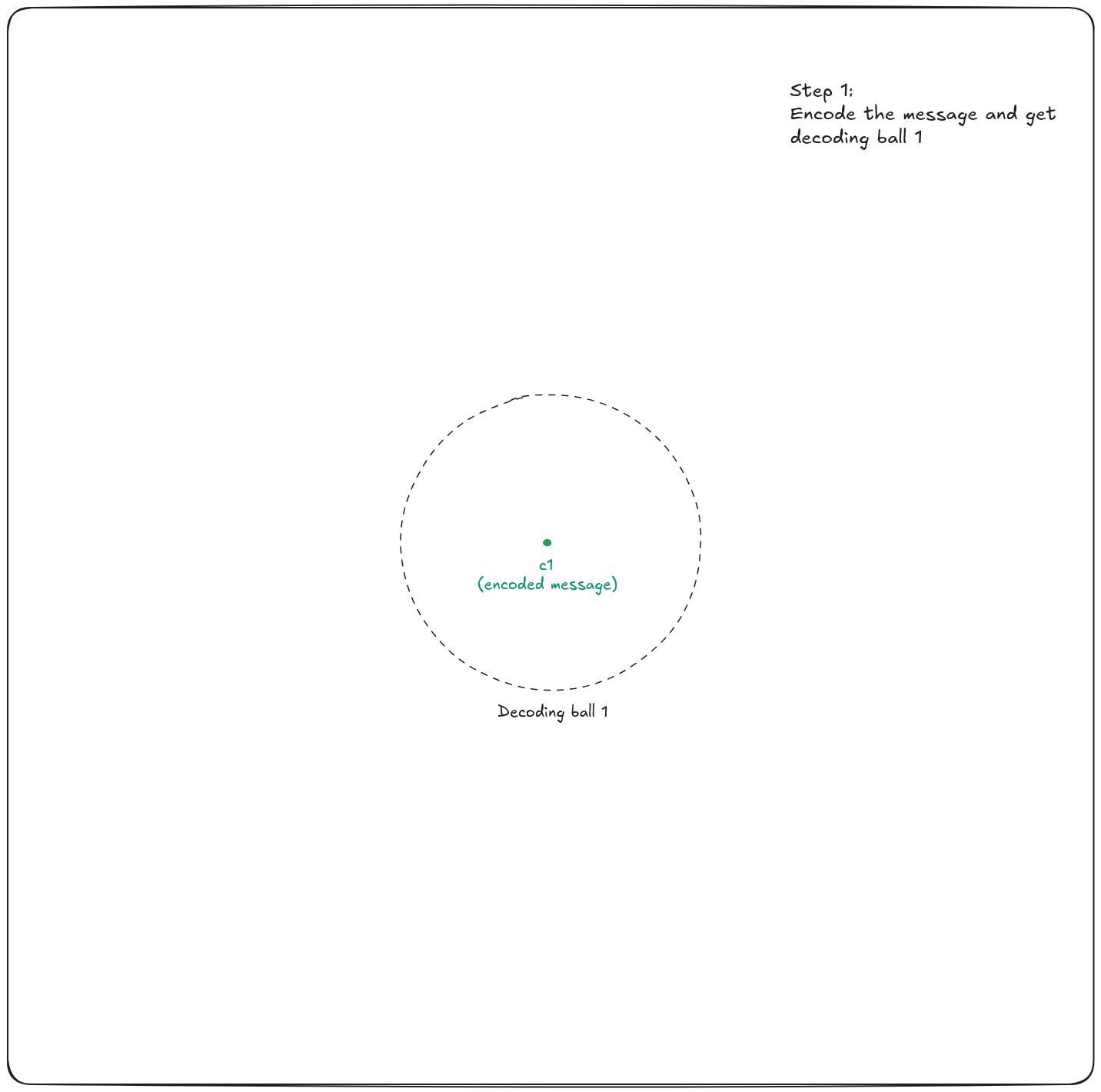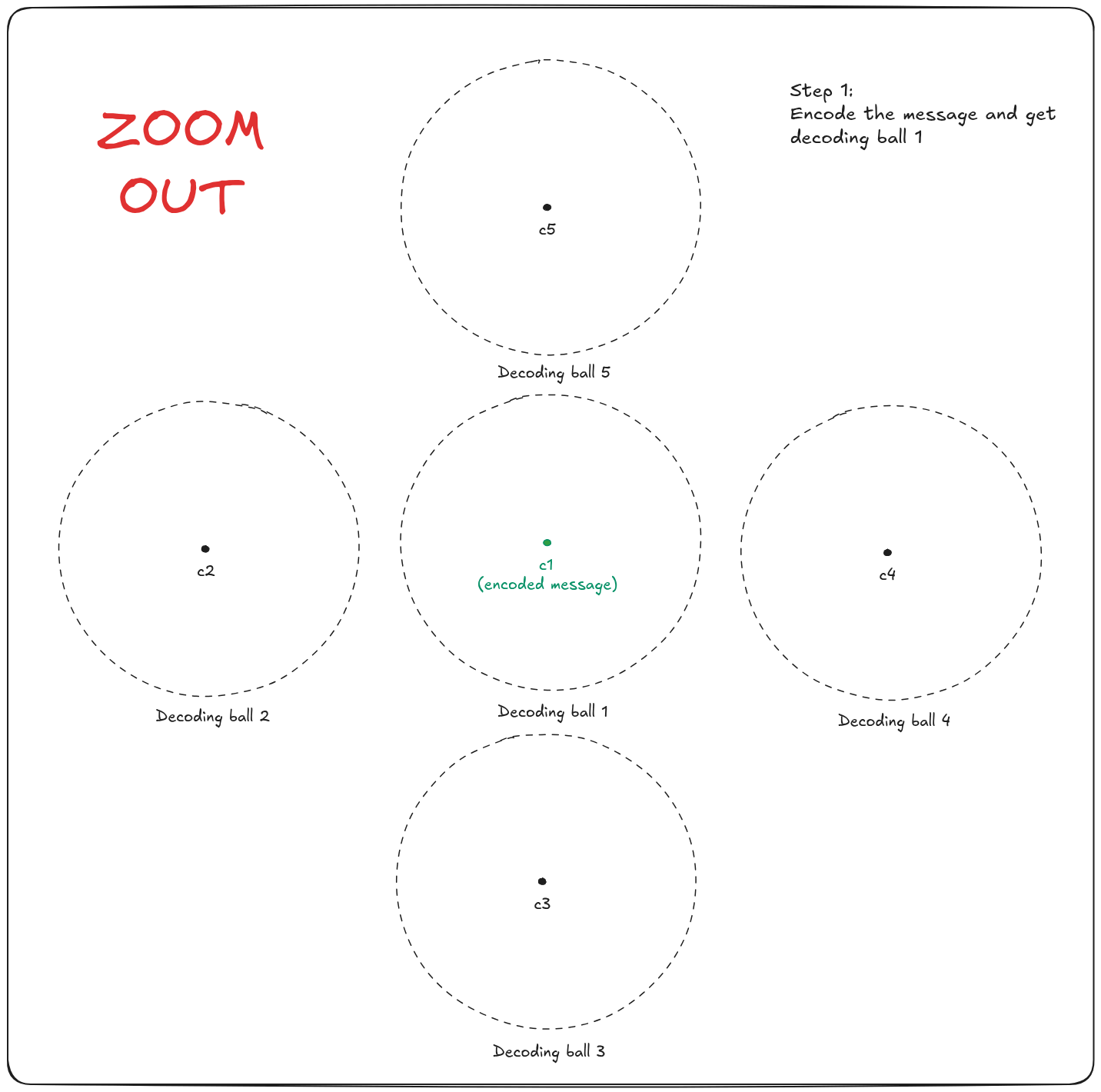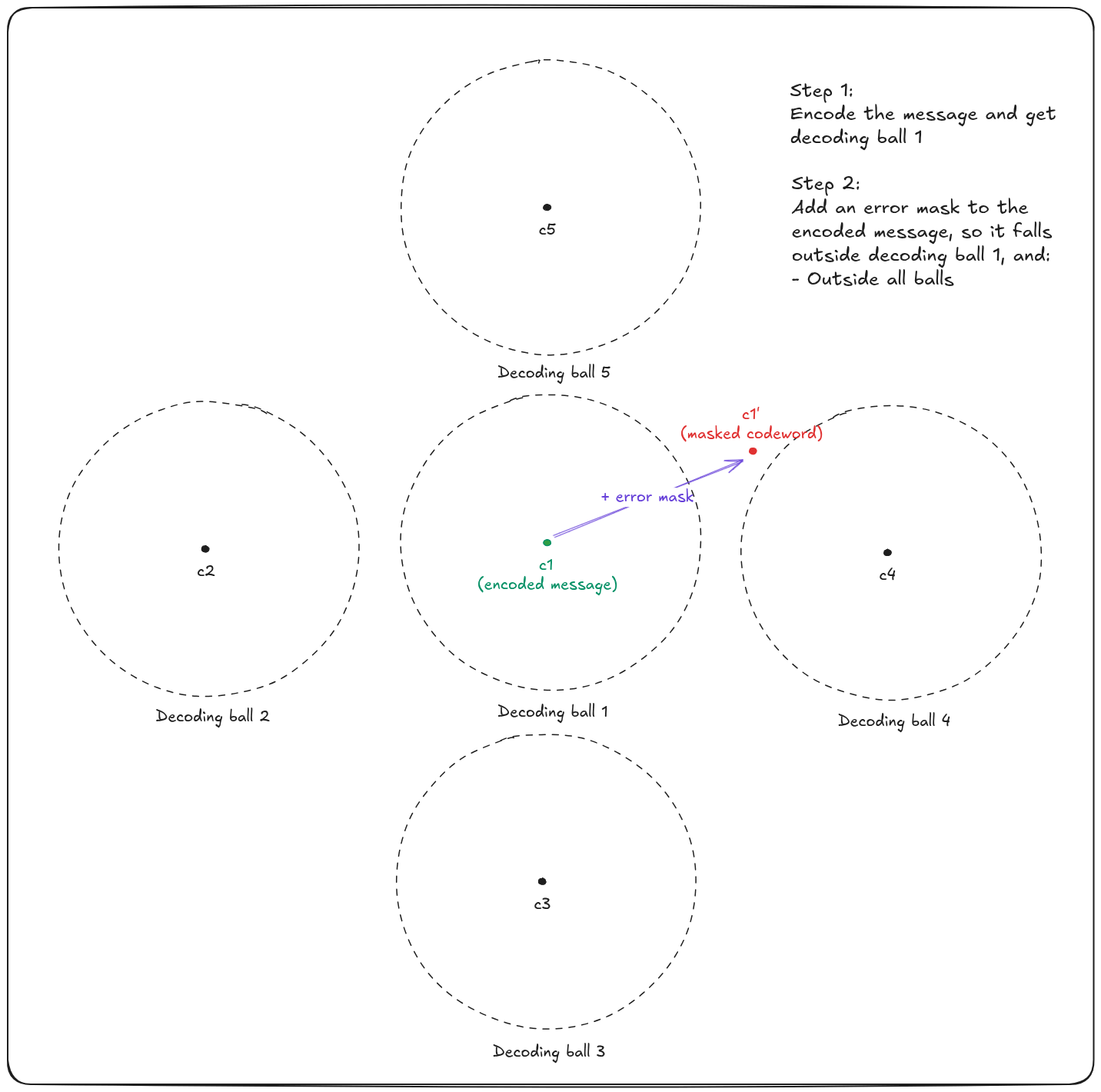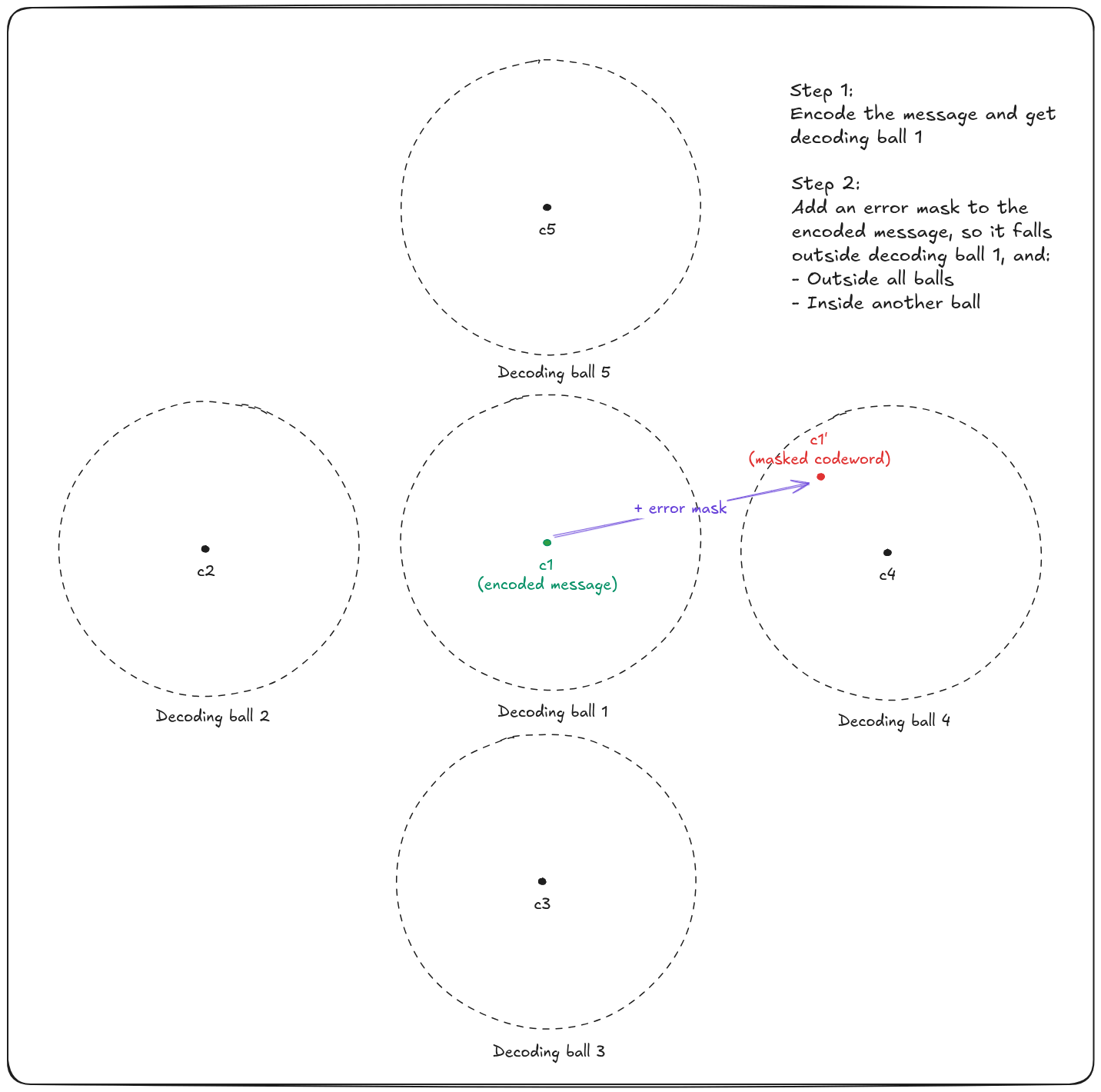
To decrypt the message, Bob needs to remove the mask to fall back into the initial decoding ball. To perform this operation, he uses his secret transformation: A trapdoor based on some private key. Then, the result is a codeword that he can correctly decode with the public code .

The hardness comes in removing the mask! Indeed, this operation cannot be done efficiently without Bob's trapdoor (which only Bob knows; this is Bob's private key). In fact, removing the mask without the trapdoor requires solving the believed hard Syndrome Decoding Problem for random Hamming Quasi-Cyclic codes, even with the help of Thanos and its magic algorithms!

You might be wondering:

• What are the private and public information inside HQC?
• What is the public code? You will find answers to your questions inside the specification and the Python implementation ;)

Endgame

Happily, the Avengers watch over our security and repel Thanos. I am wondering if there might be strong connections between NIST and Avengers...

Any resemblance to real persons living or dead is purely coincidental.

Edited by Pierre-Yvan Liardet and Jad Zahreddine